
题目列表(包括答案和解析)
21、(本小题满分12分)
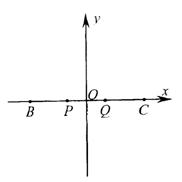
在ΔABC中,已知B(-3,0),C(3,0),AD⊥BC于D,ΔABC的垂心H分有向线段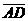 所成的比为
所成的比为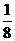 .
.
(Ⅰ)求点H的轨迹方程;
(Ⅱ)设P(-1,0),Q(1,0),那么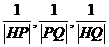 能成等差数列吗?为什么?
能成等差数列吗?为什么?
20、(本小题满分12分)
如图是一个计算机装置示意图,A、B是数据输入口,C是计算结果的输出口,计算过程是由A,B分别输入正整数m和n,经计算得正整数k,然后由C输出,即f(m,n)=k.此种计算装置完成的计算满足以下三个性质:
①若A,B分别输入1,则输出结果为2,即f(1,1)=2;
②若A输入1,B的输入由n变为n+1,则输出结果比原来增大2,即f(1,n+1)=f(1,n)+2;
③若B输入n,A的输入由m变为m+1,则输出结果为原来的3倍,即f(m+1,n)=3f(m,n).
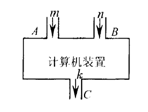 试回答下列问题:
试回答下列问题:
(Ⅰ)若A输入2,B输入3,则输出的结果为多少?
(Ⅱ)若A输入1,B输出入n(n∈N*),则输出的结果为多少?
(Ⅲ)由C能输出多少个不同的两位数?
19、(本小题满分12分)
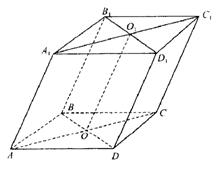
如图,已知斜平行六面体ABCD-A1B1C1D1中,AB=AD,∠A1AB=∠A1AD=∠BAD.
(Ⅰ)求证:平面B1D1DB⊥平面A1C1CA;
(Ⅱ)当A1B1=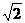 ,且直线A1A到平面B1D1DB的距离为1时,求∠BAD的大小.
,且直线A1A到平面B1D1DB的距离为1时,求∠BAD的大小.
18、(本小题满分12分)
已知a<1,解关于x的不等式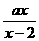 >1.
>1.
17、(本小题满分12分)
已知向量a=e1-e2,b=4e1+3e2,其中e1=(1,0),e2=(0,1).
(Ⅰ)试计算a·b及 | a+b | 的值;
(Ⅱ)求向量a的夹角b的大小.
16、某招呼站,每天均有3辆开往省城南京的分为上、中、下等级的客车. 某天袁先生准备在该招呼站乘车前往南京办事,但他不知道道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆. 那么他乘上上等车的概率为 .
15、已知A、B为锐角,且满足tanA·tanB=tanA+tanB+1,则cos (A+B)= .
14、给出以下几个命题:
①如果空间两条直线与第三条直线所成的角相等,那么这两条直线平行;
②如果空间两个平面都垂直于第三个平面,那么这两个平面平行;
③空间中,到定点距离等于定长的点的轨迹是圆;
④正三棱锥两侧面所成的二面角大于60°.
其中,正确命题的序号为 .
13、曲线y=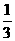 x3在点(1,
x3在点(1,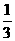 )处的切线与直线x+y-3=0的夹角为
.
)处的切线与直线x+y-3=0的夹角为
.
12、定义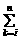 ak=ai+ai+1+…+an,其中i,n∈N,且i≤n.若f(x)=
ak=ai+ai+1+…+an,其中i,n∈N,且i≤n.若f(x)=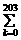 (-1)kCk2003(3- x)k=
(-1)kCk2003(3- x)k=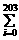 aix2003-I,则
aix2003-I,则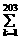 ak的值为
ak的值为
A、2 B、3 C、-1 D、-2
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com