
题目列表(包括答案和解析)
171. 如图:已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q。
 求证:P、Q、R三点共线。
求证:P、Q、R三点共线。
解析:点在线上,线在面内,可得点在面内,证明P,Q,R三个点是平面
 与平面ABC的公共点,即可。
与平面ABC的公共点,即可。
22.(本小题共14分)已知函数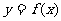 的图象经过坐标原点,且
的图象经过坐标原点,且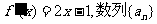 的前
的前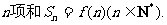
(I)求数列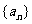 的通项公式;
的通项公式;
(II)若数列 满足
满足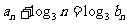 ,求数列
,求数列 的前n项和。
的前n项和。
(Ⅲ)设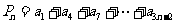 ,
,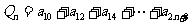 ,其中
,其中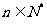 ,试比较
,试比较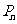 与
与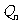 的大小,并证明你的结论。
的大小,并证明你的结论。
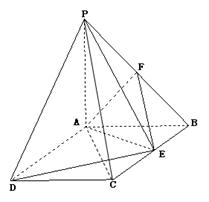
21.(本小题满分12分) 如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1, AD=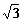 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.
20.(本小题12分)某乡镇为了盘活资本,优化组合,决定引进资本拯救出现严重亏损的企业。长年在外经商的王先生为了回报家乡,决定投资线路板厂和机械加工厂。王先生经过预算,如果引进新技术在优化管理的情况下,线路板厂和机械加工厂可能的最大盈利率分别为95﹪和80﹪,可能的最大亏损率分别为30﹪和10﹪。由于金融危机的影响,王先生决定最多出资100万元引进新技术,要求确保可能的资金亏损不超过18万元.问王先生对线路板厂和机械加工厂各投资多少万元,才能使可能的盈利最大?
19.(本小题12分) 欣欣服装厂在2010年第一季度共生产A、B、C三种品牌的男女休闲服装2000件,如下表所示
|
品牌 |
A |
B |
C |
|
女服装 |
373 |
x |
y |
|
男服装 |
377 |
370 |
z |
现从这些服装中随机抽取一件进行检验,已知抽到品牌B女服装的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在生产的这些服装中随机抽取48件进行检验,问应在品牌C中抽取多少件?
(3)已知y 245,z
245,z 245,求品牌C中生产的女服装比男服装多的概率.
245,求品牌C中生产的女服装比男服装多的概率.
18.(本小题满分12分) 已知函数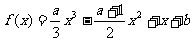 ,其中
,其中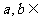 R.
R.
(Ⅰ)若曲线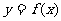 在点
在点 处的切线方程为
处的切线方程为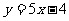 ,求函数
,求函数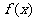 的解析式;
的解析式;
(Ⅱ)当 时,讨论函数
时,讨论函数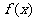 的单调性.
的单调性.
17.(本题满分12分)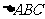 中内角
中内角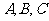 的对边分别为
的对边分别为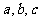 ,向量
,向量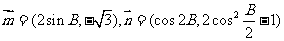 且
且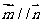
(Ⅰ)求锐角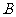 的大小,
的大小,
(Ⅱ)如果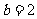 ,求
,求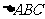 的面积
的面积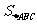 的最大值
的最大值
16.设函数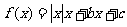 ,给出下列4个命题:
,给出下列4个命题:
①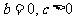 时,方程
时,方程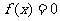 只有一个实数根;
只有一个实数根;
②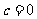 时,
时,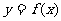 是奇函数;
是奇函数;
③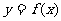 的图象关于点
的图象关于点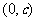 对称;
对称;
④函数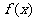 至多有2个零点。
至多有2个零点。
上述命题中的所有正确命题的序号是 .
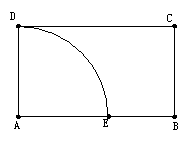
15.如图,四边形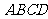 为矩形,
为矩形,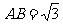 ,
,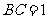 ,以
,以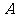 为圆心,1为半径作四分之一个圆弧
为圆心,1为半径作四分之一个圆弧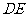 ,在圆弧
,在圆弧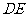 上任取一点
上任取一点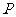 ,则直线
,则直线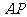 与线段
与线段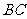 有公共点的概率是
有公共点的概率是
14.过椭圆C: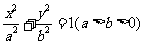 的一个顶点作圆
的一个顶点作圆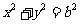 的两条切线, 切点分别为A,B,若
的两条切线, 切点分别为A,B,若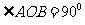 (O是坐标原点),则椭圆C的离心率为
(O是坐标原点),则椭圆C的离心率为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com