
题目列表(包括答案和解析)
2.答案:D解析:设二级品有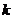 个,∴ 一级品有
个,∴ 一级品有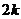 个,三级品有
个,三级品有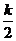 个,总数为
个,总数为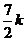 个。
个。
∴ 分布列为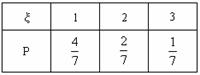
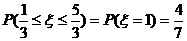
1. 答案:B;[解题思路]: 由离散型随机变量分布列的性质可得
解析:由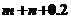
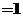 ,又
,又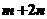
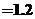 ,可得
,可得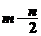
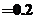
[名师指引]离散型随机变量的分布列都具有下面两个性质:
⑴Pi≥0,i=1,2,…;
⑵P1+P2+…=1.
2. 甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为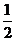 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是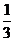 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率; (2)签约人数 的分布列和数学期望.
的分布列和数学期望.
高三数学章节训练题28《随机变量及其分布》答案
1. 若随机事件A在1次试验中发生的概率是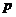 ,用随机变量
,用随机变量 表示A在1次实验中发生的次数。(1)求方差
表示A在1次实验中发生的次数。(1)求方差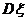 的最大值;(2)求
的最大值;(2)求 的最大值.
的最大值.
4. 设 是一个离散型随机变量,其分布列如下表,则
是一个离散型随机变量,其分布列如下表,则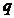 =
.
=
.
 |
-1 |
0 |
1 |
|
P |
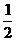 |
1-2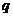 |
 |
3. 同时掷两枚骰子,它们各面分别刻有: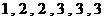 ,若
,若 为掷得点数之积,则
为掷得点数之积,则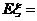 .
.
2. 一袋中装有4个白球,2个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现3次停止,设停止时,取球次数为随机变量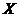 ,则
,则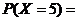 ________.
________.
1. 甲、乙两人对同一目标各射击一次,甲、乙命中的概率分别为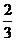 和
和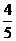 ,若命中目标的人数为
,若命中目标的人数为 ,则
,则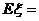 .
.
6. 设 是离散型随机变量,
是离散型随机变量,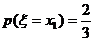 ,
,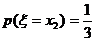 ,且
,且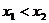 ,现已知:
,现已知: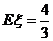 ,
,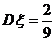 ,则
,则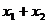 的值为( )
的值为( )
A.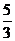 B.
B.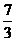 C.3
D.
C.3
D.
5. 随机变量 的所有等可能取值为
的所有等可能取值为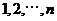 ,若
,若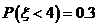 ,则( )
,则( )
A.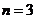 ; B.
; B.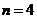 ; C.
; C.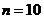 ; D.不能确定
; D.不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com