
题目列表(包括答案和解析)
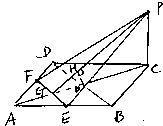
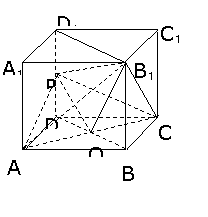
240. 如图,在正方体ABCD-A1B1C1D1中,E、F、G、H、L、M、N分别是A1D1、A1B1、BC、CD、DA、DE、CL的中点,(1)求证:EF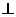 GF;(2)求证:MN//平面EFGH;(3)若AB=2,求MN到平面EFGH的距离。
GF;(2)求证:MN//平面EFGH;(3)若AB=2,求MN到平面EFGH的距离。
解:(1)证:取B1C1中点Q,则GQ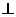 面A1B1C1D1,且EF
面A1B1C1D1,且EF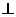 FQ,由三垂线定理得EF
FQ,由三垂线定理得EF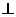 GF;
GF;
(2)在三角形DEG中,MN//EG,由此可证MN//平面EFGH;
(3)设所求距离为h,由VE-NGH=VN-HEG,得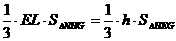 ,又
,又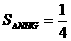 ,
,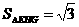 ,EL=2,故
,EL=2,故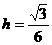 。
。
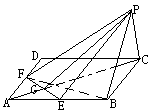
239.已知:如图,ABCD是边长为2的正方形,
PC⊥面ABCD,PC=2,E、F是AB、AD中点。
求:点B到平面PEF的距离。
解析:由BD∥EF可证DB∥平面PEF,则点B到平面PEF的距离转化为直线与平面PEF的距离。又由平面PCA垂直平面PEF,故DB与AC的交点到两垂直平面的交线的距离为所求距离。
方法一:连接DB,AC交于O点,设AC交EF于G,连PG,
作OH⊥PG,H为垂足。
∵E、F是AB、AD中点,∴EF∥DB,∴DB∥面PEF,
∵ABCD是正方形,∴AC⊥BD,∴EF⊥AC,
∵PC⊥面ABCD,∴EF⊥PC,∴EF⊥面PCG,
∵EFÌ面PEF,∴面PEF⊥面PCG,
∵OH⊥PG,∴OH⊥面PEF,即OH为所求点B到平面PEF的距离。
由ABCD边长为2,∴AC=2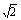 ,GO=
,GO=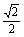 ,GC=
,GC=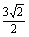 ,
,
∵PC⊥面ABCD,∴PC⊥AC,
∴△OHG∽△PCG,∴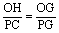 ,
,
由PC=2,PG=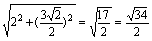
∴OH=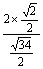 =
=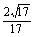
即点B到平面PEF的距离为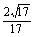 。
。
方法二:如图,连接BF、PB,设点B到平面PEF的距离为d,
 由VP-BEF=
由VP-BEF=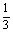 S△BEF·PC
S△BEF·PC
=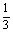 ×
×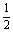 ×BE×AF×PC
×BE×AF×PC
=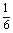 ×1×1×2=
×1×1×2=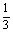
连AC交EF于G,连PG,由方法一知
PG=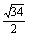 ,EF=
,EF=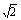 ,S△PEF=
,S△PEF=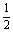 ×
×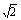 ×
×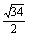 =
=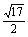
∴VB-PEF=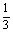 ·S△PEF·d=VP-BEF=
·S△PEF·d=VP-BEF=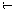 ,
,
∴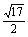 d=1
d=
d=1
d=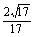
即点B到平面PEF的距离为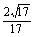 。
。
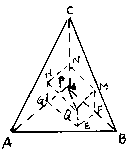
238. 三棱锥P-ABC的三条侧棱PA、PB、PC两两垂直,底面ABC上一点Q到侧面PAB、侧面PBC、侧面PAC的距离依次为2,3,6。
 求:P、Q两点间的距离。
求:P、Q两点间的距离。
解析:如图,作QE⊥面PAB,
QM⊥面PBC,QH⊥面PAC,E、M、N为垂足。
由PA、PB、PC两两垂直,所以PC⊥面PAB,PB⊥面PAC,
PA⊥面PBC,可得三个侧面两两垂直。
设平面QEM与PB交于F,平面QEH与PA交于G,平面MQH与PC交于N,连接EF、MF、GH、GQ、NH、NM,可证明QMNH-EFPG是长方体。
∴PQ=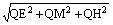 =
=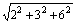 =7。
=7。
237. 正方体各个面所在的平面能将空间分成m个部分,m应等于 ( ) A. 27 B. 21 C. 18 D.9
解析:A
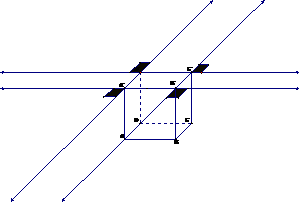 如果将正方体各个面延展,可视为将空间分成三个层面,上面如图标出直角的层面,中间一层,下面一层,而上面一个层面中,又分成九个部分,共9
如果将正方体各个面延展,可视为将空间分成三个层面,上面如图标出直角的层面,中间一层,下面一层,而上面一个层面中,又分成九个部分,共9 3=27个部分。
3=27个部分。
236. 在正方体ABCD-A1B1C1D1中,P为DD1中点,O为底面ABCD中心, 求证:B1O⊥平面PAC。
证明:如图:连结AB1,CB1,设AB=1
∵AB1=CB1=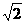 ,AO=CO,∴B1O⊥AC,
连结PB1,∵
,AO=CO,∴B1O⊥AC,
连结PB1,∵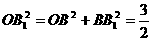
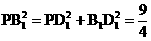
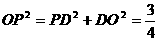 ∴
∴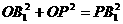 ∴B1O⊥PO,
∴B1O⊥平面PAC。
∴B1O⊥PO,
∴B1O⊥平面PAC。
233. 如图:BC是Rt△ABC的斜边,AP⊥平面ABC,连结PB、PC,作PD⊥BC于D,连结AD,则图中共有直角三角形_________个。
8
解析:Rt△PAB、Rt△PAC、Rt△ABC、Rt△ADP。
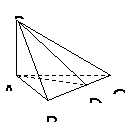 可证BC⊥平面APD,由BC⊥AD,BC⊥PD
可得Rt△PBD、Rt△PDC、Rt△ADB、Rt△ADC
共8个。
234. 如图:已知ABCD是空间四边形,AB=AD,CB=CD
求证:BD⊥AC
可证BC⊥平面APD,由BC⊥AD,BC⊥PD
可得Rt△PBD、Rt△PDC、Rt△ADB、Rt△ADC
共8个。
234. 如图:已知ABCD是空间四边形,AB=AD,CB=CD
求证:BD⊥AC
 证明:设BD的中点为K,连结AK、CK,
∵AB=AD,K为BD中点
∴AK⊥BD
同理CK⊥BD,且AK∩KC=K
∴BD⊥平面AKC
∴BD垂直于平面AKC内的所有直线
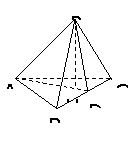
235. 如图2-40:P是△ABC所在平面外的一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC,H是垂足。
求证:H是ABC的垂心。
证明:设BD的中点为K,连结AK、CK,
∵AB=AD,K为BD中点
∴AK⊥BD
同理CK⊥BD,且AK∩KC=K
∴BD⊥平面AKC
∴BD垂直于平面AKC内的所有直线
235. 如图2-40:P是△ABC所在平面外的一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC,H是垂足。
求证:H是ABC的垂心。
 证明:∵PA⊥PB,PB⊥PC,
证明:∵PA⊥PB,PB⊥PC,
 ∴PA⊥平面PBC,BC
∴PA⊥平面PBC,BC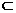 平面PBC
∴BC⊥PA
∵PH⊥平面ABC,BC
平面PBC
∴BC⊥PA
∵PH⊥平面ABC,BC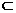 平面ABC
∴BC⊥PH
∴BC⊥平面PAH,AH
平面ABC
∴BC⊥PH
∴BC⊥平面PAH,AH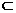 平面PAH
∴AH⊥BC,同理BH⊥AC,CH⊥AB,
因此H是△ABC的垂心。
平面PAH
∴AH⊥BC,同理BH⊥AC,CH⊥AB,
因此H是△ABC的垂心。
232.如图:已知PA⊥⊙O所在的平面,AB是⊙O的直径,
C是异于A、B的⊙O上任意一点,过A作AE⊥PC于E ,
求证:AE⊥平面PBC。
证明:∵PA⊥平面ABC,∴PA⊥BC,
又∵AB是⊙O的直径,∴BC⊥AC
而PA∩AC=A,∴BC⊥平面PAC
又∵AE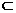 平面PAC,∴BC⊥AE
∵PC⊥AE且PC∩BC=C,∴AE⊥平面PBC。
平面PAC,∴BC⊥AE
∵PC⊥AE且PC∩BC=C,∴AE⊥平面PBC。
231.如图2-35:在空间四边形ABCD中,已知BC=AC,AD=BD,引BE⊥CD,E为垂足,作AH⊥BE于H,求证:AH⊥平面BCD。
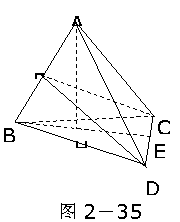 解析: 要证AH⊥平面BCD,只须利用直线和平面垂直的判定定理,证AH垂直于平面BCD中两条相交直线即可。
解析: 要证AH⊥平面BCD,只须利用直线和平面垂直的判定定理,证AH垂直于平面BCD中两条相交直线即可。
证明:取AB中点F,连结CF、DF,
∵AC=BC,∴CF⊥AB,
又∵AD=BD,∴DF⊥AB,∴AB⊥平面CDF,
又CD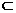 平面CDF,∴CD⊥AB
又CD⊥BE,∴CD⊥平面ABE,CD⊥AH
又AH⊥BE,∴AH⊥平面BCD。
平面CDF,∴CD⊥AB
又CD⊥BE,∴CD⊥平面ABE,CD⊥AH
又AH⊥BE,∴AH⊥平面BCD。
 点评:证明线面垂直,需转化为线线垂直,而线线垂直,又可通过证线面垂直来实现。在这里,定义可以双向使用,即直线a垂直于平面α内的任何直线,则a⊥α,反之,若a⊥α,则a垂直于平面α内的任何直线。
点评:证明线面垂直,需转化为线线垂直,而线线垂直,又可通过证线面垂直来实现。在这里,定义可以双向使用,即直线a垂直于平面α内的任何直线,则a⊥α,反之,若a⊥α,则a垂直于平面α内的任何直线。
250. 分别和两条异面直线都相交的两条直线的位置关系是( )
A.平行 B.异面 C.平行或异面 D.相交或异面
解析:本题考查两条直线的位置关系,异面直线的概念,以及空间想象能力.
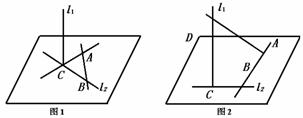
解法一:设两条异面直线分别为l1,l2,则与它们分别相交的两条直线有可能相交,如图1,也可能异面,如图2,它们不可能平行,这是由于:假设这两条直线平行,则它们确定一个平面α,两条平行线与两条异面直线l1与l2的四个交点均在α内,则两异面直线l1与l2也在α内,这是不可能的.∴应选D.
解法二:利用排除法,容易发现,分别和两条异面直线都相交的两条直线可以是相交的位置关系,由于这点可以排除选择选A、B、C.故选D.
249. 如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有( )
A.12对 B.24对 C.36对 D.48对
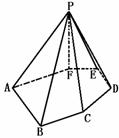
解析:本题以六棱锥为依托,考查异面直线的概念及判断,以及空间想象能力.
解法一:如图,任何两条侧棱不成异面直线,任何两条底面上的棱也不成异面直线,所以,每对异面直线必然其中一条是侧棱而另一条为底面的棱,每条侧棱,可以且只有与4条底面上的棱组成4对异面直线,又由共6条侧棱,所以异面直线共6×4=24对.
解法二:六棱锥的棱所在12条直线中,能成异面直线对的两条直线,必定一条在底面的平面内,另一条是侧棱所在直线.底面棱所在直线共6条,侧棱所在直线也有6条,各取一条配成一对,共6×6=36对,因为,每条侧棱所在的直线,与底面内的6条直线有公共点的都是2条,所以,在36对中不成异面直线的共有6×2=12对.所以,六棱锥棱所在的12条直线中,异面直线共有36-12=24对.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com