9．若关于x的方程3x²－5x+a＝0的一个根在(－2,0)内，另一个根在(1,3)内，则a的取值范围是________．

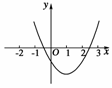
图1

解析：设f(x)＝3x²－5x+a(如图1所示)，则f(x)＝0的两根分别在(－2,0)、(1,3)内的充要条件是

解之，得－12<a<0.

答案：(－12,0)

8．已知A＝[1，b](b>1)，对于f(x)＝(x－1)²+1，当x∈A时，f(x)∈A，则b的值是__________．

解析：x∈[1，b]时，f(x)是增函数，故x＝b时，f(x)取最大值，即f(b)＝b，得(b－1)²+1＝b，解得b＝3或b＝1(舍去)．

答案：3

7．若f(x)＝g(x)＝x²－x(x∈R)，则方程f[g(x)]＝x的解为__________．

解析：当g(x)＝x²－x≥2，即x≤－1或x≥2时，方程f[g(x)]＝x可变为x²－x－1＝x，解得x＝1+.

当g(x)＝x²－x<2，即－1<x<2时，方程f[g(x)]＝x可变为x＝1.

所以方程f[g(x)]＝x的解为x＝1或x＝1+.

答案：x＝1或x＝1+

6．(2009·宁夏银川一模)二次函数y＝a(a+1)x²－(2a+1)x+1，当a＝1,2,3，…，n，…时，其图象在x轴上截得的弦长依次为d₁，d₂，…，d_n，…，则d₁+d₂+…+d_n为　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：令a(a+1)x²－(2a+1)x+1＝0，

解得x＝或x＝，

∴函数图象与x轴的两交点的横坐标自左至右分别为和，

∴d₁+d₂+…+d_n＝1－+－+…+－＝1－＝.

答案：D

5．已知二次函数y＝ax²+bx+c满足a>b>c，且a+b+c＝0，那么它的图象是下图中的(　)

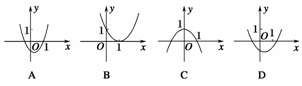
解析：首先注意到a+b+c＝0即是令解析式中x＝1得到的，即当x＝1时y＝0，也就是抛物线必过(1,0)点，因而D显然不对，又a+b+c＝0，a>b>c，可得a>0，c<0，由a>0可知C不对；由c<0可知B不对，故应选A.

答案：A

4．不等式f(x)＝ax²－x－c>0的解集为{x|－2<x<1}，则函数y＝f(－x)的图象为(　)

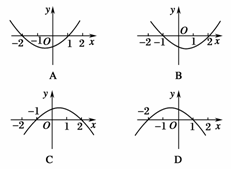
解析：由解得

∴f(x)＝－x²－x+2，∴f(－x)＝－x²+x+2，由图象知选C.

答案：C

3．已知函数f(x)＝4x²－mx+5在区间[－2，+∞)上是增函数，则f(1)的范围是(　)

A．f(1)≥25　 　　　　　　　　　　　　　　　　　 B．f(1)＝25

C．f(1)≤25　 　　　　　　　　　　　　　　　　　 D．f(1)>25

解析：y＝f(x)的对称轴是x＝，可知f(x)在[，+∞)上递增，由题设只需≤－2⇒m≤－16，

∴f(1)＝9－m≥25.

答案：A

2．已知抛物线y＝ax²+bx+c(a≠0)的图象经过一、二、四象限，则直线y＝ax+b不经过第________象限．　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．一　 　　　　　　　　　　　　　　　　　　　　　 B．二

C．三　 　　　　　　　　　　　　　　　　　　　　　 D．四

解析：由题意知∴　　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网

∴直线y＝ax+b不经过第二象限．

答案：B

1．函数f(x)＝ax²+bx+6满足条件f(－1)＝f(3)，则f(2)的值为　　　　　　　　　 　 (　)

A．5　　　　　　　　　　　　　 B．6

C．8　 　　　　　　　　　　　　　　　　　　　　　　 D．与a、b值有关

解析：由f(－1)＝f(3)知，对称轴x＝－＝1，∴b＝－2a.∴f(2)＝4a+2b+6＝4a+2×(－2a)+6＝6.

答案：B

13．(20分)(2009·上海高考)已知函数y＝f^－1(x)是y＝f(x)的反函数．定义：若对给定的实数a(a≠0)，函数y＝f(x+a)与y＝f^－1(x+a)互为反函数，则称y＝f(x)满足“a和性质”；若函数y＝f(ax)与y＝f^－1(ax)互为反函数，则称y＝f(x)满足“a积性质”．

(1)判断函数g(x)＝x²+1(x>0)是否满足“1和性质”，并说明理由；

(2)求所有满足“2和性质”的一次函数；

(3)设函数y＝f(x)(x>0)对任何a>0，满足“a积性质”．求y＝f(x)的表达式．

解：(1)函数g(x)＝x²+1(x>0)的反函数是g^－1(x)＝(x>1)，∴g^－1(x+1)＝(x>0)，

而g(x+1)＝(x+1)²+1(x>－1)，其反函数为y＝－1(x>1)，

故函数g(x)＝x²+1(x>0)不满足“1和性质”．

(2)设函数f(x)＝kx+b(x∈R)满足“2和性质”，k≠0.

∴f^－1(x)＝(x∈R)，∴f^－1(x+2)＝，

而f(x+2)＝k(x+2)+b(x∈R)，得反函数为y＝，由“2和性质”定义可知＝对x∈R恒成立，∴k＝－1，b∈R，即所求一次函数为f(x)＝－x+b(b∈R)．

(3)设a>0，x₀>0，且点(x₀，y₀)在y＝f(ax)图象上，则(y₀，x₀)在函数y＝f^－1(ax)图象上，故可得ay₀＝f(x₀)＝af(ax₀)．令ax₀＝x，则a＝，∴f(x₀)＝f(x)，即f(x)＝.

综上所述，f(x)＝(k≠0)，此时f(ax)＝，其反函数就是y＝，而f^－1(ax)＝，故y＝f(ax)与y＝f^－1(ax)互为反函数．

　　 www.k@s@5@　　　　　　　　　　　　　　 高#考#资#源#网