
题目列表(包括答案和解析)
5.(2009·南昌二模)函数f(x)=sinx在区间[a,b]上是增函数,且f(a)=-1,f(b)=1,则cos的值为
( )
A.0 B.
C.1 D.-1
解析:由f(a)=-1,f(b)=1,得a=2kπ-,k∈Z,b=2kπ+,k∈Z,且a、b中k取同一个值,故cos=cos2kπ=1,故选C.
答案:C
4.(2009·江苏苏州模拟)函数y=sin4x+cos2x的最小正周期为
( )
A. B.
C.π D.2π
解析:y=sin4x+cos2x=()2+
=+
=+=+·,
∴T==.
答案:B
3.(2009·全国卷Ⅰ)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为
( )
A. B.
C. D.
解析:依题意得3cos(+φ)=0,+φ=kπ+,φ=kπ-(k∈Z),因此|φ|的最小值是,选A.
答案:A
2.如果|x|≤,f(x)=cos2x+sinx的最小值是
( )
A. B.-
C.-1 D. www.k@s@5@ 高#考#资#源#网
解析:∵f(x)=(1-sin2x)+sinx
=-(sinx-)2+.
又∵|x|≤,∴sinx∈[-,],
故当sinx=-时,
[f(x)]min=1-(-)2+(-)=.
答案:D
1.(2009·四川高考)已知函数f(x)=sin(x-)(x∈R),下面结论错误的是
( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间[0,]上是增函数
C.函数f(x)的图象关于直线x=0对称
D.函数f(x)是奇函数
解析:∵f(x)=sin(x-)=-cosx(x∈R),∴函数f(x)是最小正周期为2π的偶函数,故选D.
答案:D
22.(满分14分)
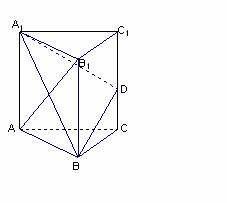 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为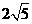 ,设这条最短路线与CC1的交点为D. K^S*5U.C#
,设这条最短路线与CC1的交点为D. K^S*5U.C#
(Ⅰ)求三棱柱ABC-A1B1C1的体积;
(Ⅱ)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(Ⅲ)证明:平面A1BD⊥平面A1ABB1
21.(满分12分)
在棱长为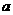 的正方体
的正方体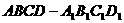 中,
中,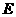 、
、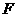 分别是
分别是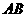 、
、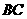 的中点,
的中点,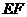 与
与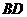 交于点
交于点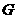 ,
,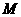 为棱上
为棱上 一点.
一点.
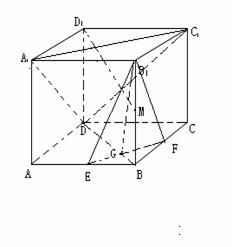 (Ⅰ)
(Ⅰ)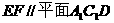 ;
;
(Ⅱ)当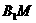 :
: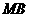 的值为多少时,
的值为多少时,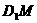 ⊥平面
⊥平面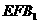 ,证明之;
,证明之;
(Ⅲ)求点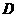 到平面
到平面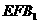 的距离.
的距离.
20.(满分12分)
如图(1),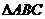 是等腰直角三角形,
是等腰直角三角形,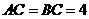 ,
,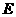 、
、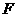 分别为
分别为 、
、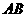 的中点,将
的中点,将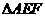 沿
沿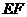 折起,使
折起,使 在平面
在平面 上的射影
上的射影 恰为
恰为 的中点,得到图(2).
的中点,得到图(2).
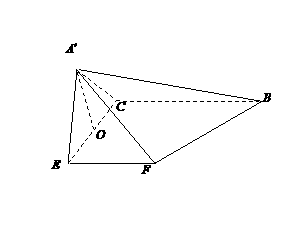 (Ⅰ)求证:
(Ⅰ)求证: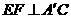 ;
;
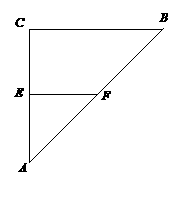 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥 的体积.
的体积.
图(1) 图(2)
19. (满分12分)
(满分12分)
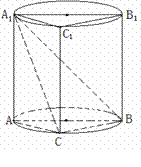
如图组合体中,三棱柱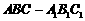 的侧面
的侧面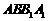 是圆柱的轴截面,
是圆柱的轴截面,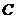 是圆柱底面圆周上不与
是圆柱底面圆周上不与 、
、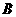 重合一个点.
重合一个点.
(Ⅰ)求证:无论点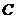 如何运动,平面
如何运动,平面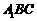
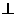 平面
平面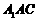 ;
;
(Ⅱ)当点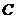 是弧
是弧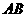 的中点时,求四棱锥
的中点时,求四棱锥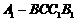 与圆柱的体积比.
与圆柱的体积比.
18.(满分12分)
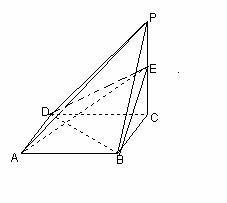
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(Ⅰ)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(Ⅱ)若点E为PC的中点,求证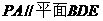 ;
;
(III)求由点A绕四棱锥P-ABCD的侧面一周回到点A的最短距离
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com