
题目列表(包括答案和解析)
4.圆锥曲线的几何性质:
(1)椭圆(1)若椭圆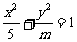 的离心率
的离心率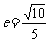 ,则
,则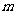 的值是__(答:3或
的值是__(答:3或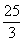 );(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答:
);(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答: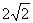 )
)
(2)双曲线(1)双曲线的渐近线方程是 ,则该双曲线的离心率等于______(答:
,则该双曲线的离心率等于______(答: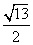 或
或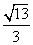 );(2)双曲线
);(2)双曲线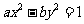 的离心率为
的离心率为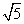 ,则
,则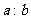 = (答:4或
= (答:4或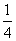 );(3)设双曲线
);(3)设双曲线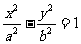 (a>0,b>0)中,离心率e∈[
(a>0,b>0)中,离心率e∈[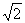 ,2],则两条渐近线夹角θ的取值范围是________(答:
,2],则两条渐近线夹角θ的取值范围是________(答: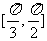 );
);
(3)抛物线;设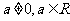 ,则抛物线
,则抛物线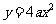 的焦点坐标为________(答:
的焦点坐标为________(答: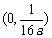 );
);
3.圆锥曲线焦点位置的判断:
椭圆:已知方程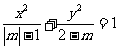 表示焦点在y轴上的椭圆,则m的取值范围是__(答:
表示焦点在y轴上的椭圆,则m的取值范围是__(答: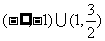 )
)
2.圆锥曲线的标准方程
(1)椭圆:(1)已知方程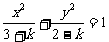 表示椭圆,则
表示椭圆,则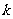 的取值范围为____(答:
的取值范围为____(答: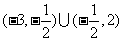 );(2)若
);(2)若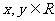 ,且
,且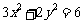 ,则
,则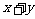 的最大值是____,
的最大值是____,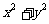 的最小值是___(答:
的最小值是___(答: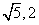 )
)
(2)双曲线:(1)双曲线的离心率等于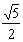 ,且与椭圆
,且与椭圆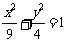 有公共焦点,则该双曲线的方程_______(答:
有公共焦点,则该双曲线的方程_______(答: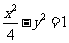 );(2)设中心在坐标原点
);(2)设中心在坐标原点 ,焦点
,焦点 、
、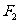 在坐标轴上,离心率
在坐标轴上,离心率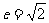 的双曲线C过点
的双曲线C过点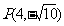 ,则C的方程为_______(答:
,则C的方程为_______(答: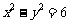 )
)
(3)抛物线:
1.圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:(1)已知定点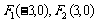 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.
,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.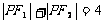 B.
B.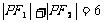 C.
C.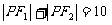 D.
D. (答:C);(2)方程
(答:C);(2)方程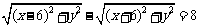 表示的曲线是_____(答:双曲线的左支)
表示的曲线是_____(答:双曲线的左支)
(2)第二定义已知点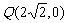 及抛物线
及抛物线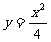 上一动点P(x,y),则y+|PQ|的最小值是_____(答:2)
上一动点P(x,y),则y+|PQ|的最小值是_____(答:2)
14、圆的切线与弦长:
设A为圆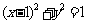 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答:
上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答: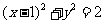 );
);
(2)弦长问题:
13、圆与圆的位置关系
双曲线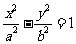 的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切)
的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切)
12、直线与圆的位置关系:(1)圆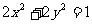 与直线
与直线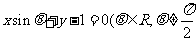
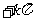 ,
,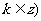 的位置关系为____(答:相离);(2)若直线
的位置关系为____(答:相离);(2)若直线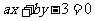 与圆
与圆 切于点
切于点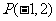 ,则
,则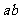 的值____(答:2);(3)直线
的值____(答:2);(3)直线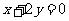 被曲线
被曲线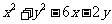
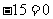 所截得的弦长等于 (答:
所截得的弦长等于 (答: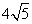 );(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 (答:4);(5)已知
);(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 (答:4);(5)已知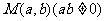 是圆
是圆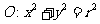 内一点,现有以
内一点,现有以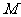 为中点的弦所在直线
为中点的弦所在直线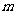 和直线
和直线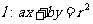 ,则A.
,则A. ,且
,且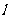 与圆相交 B.
与圆相交 B.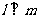 ,且
,且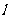 与圆相交 C.
与圆相交 C. ,且
,且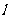 与圆相离 D.
与圆相离 D.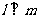 ,且
,且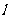 与圆相离(答:C);(6)已知圆C:
与圆相离(答:C);(6)已知圆C: ,直线L:
,直线L: 。①求证:对
。①求证:对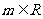 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若
,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若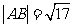 ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:②
,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:②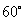 或
或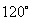 ③最长:
③最长: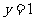 ,最短:
,最短: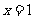 )
)
11、点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______(答: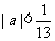 )
)
10、圆的方程:
(1)圆C与圆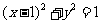 关于直线
关于直线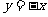 对称,则圆C的方程为____________(答:
对称,则圆C的方程为____________(答: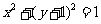 );(2)圆心在直线
);(2)圆心在直线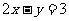 上,且与两坐标轴均相切的圆的标准方程是__________(答:
上,且与两坐标轴均相切的圆的标准方程是__________(答: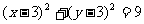 或
或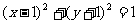 );(3)已知
);(3)已知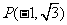 是圆
是圆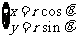 (
(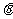 为参数,
为参数,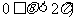 上的点,则圆的普通方程为________,P点对应的
上的点,则圆的普通方程为________,P点对应的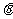 值为_______,过P点的圆的切线方程是___________(答:
值为_______,过P点的圆的切线方程是___________(答: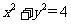 ;
;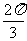 ;
;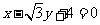 );(4)如果直线
);(4)如果直线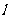 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么
将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么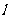 的斜率的取值范围是____(答:[0,2]);(5)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____(答:
的斜率的取值范围是____(答:[0,2]);(5)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____(答: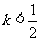 );(6)若
);(6)若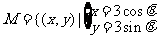 (
(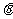 为参数,
为参数, ,
,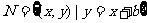 ,若
,若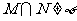 ,则b的取值范围是_________(答:
,则b的取值范围是_________(答: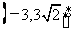 )
)
9、简单的线性规划:
已知点A(-2,4),B(4,2),且直线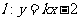 与线段AB恒相交,则
与线段AB恒相交,则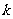 的取值范围是__________(答:
的取值范围是__________(答: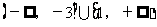 )
)
(1)线性目标函数z=2x-y在线性约束条件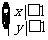 下,取最小值的最优解是____(答:(-1,1));(2)点(-2,
下,取最小值的最优解是____(答:(-1,1));(2)点(-2,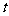 )在直线2x-3y+6=0的上方,则
)在直线2x-3y+6=0的上方,则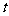 的取值范围是_________(答:
的取值范围是_________(答: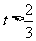 );(3)不等式
);(3)不等式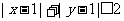 表示的平面区域的面积是_________(答:8);(4)如果实数
表示的平面区域的面积是_________(答:8);(4)如果实数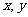 满足
满足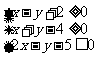 ,则
,则 的最大值_________(答:21)
的最大值_________(答:21)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com