
题目列表(包括答案和解析)
1. 已知函数y = f (x)(x∈R,x≠0)对任意的非零实数 ,
,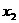 ,恒有f(
,恒有f(
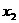 )=f(
)=f( )+f(
)+f(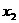 ),
),
试判断f(x)的奇偶性。
2 已知定义在[-2,2]上的偶函数,f (x)在区间[0,2]上单调递减,若f (1-m)<f (m),求实数m的取值范围
40. 某企业进行技术改造,有两种方案,甲方案:一次性贷款10万元,第一年便可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元;两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,试比较两种方案中,哪种获利更多?
(取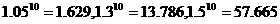 )
)
39. (1)设 是各项均不为零的
是各项均不为零的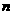 (
( )项等差数列,且公差
)项等差数列,且公差 ,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列.
,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列.
(i)当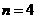 时,求
时,求 的数值;
的数值;
(ii)求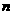 的所有可能值.
的所有可能值.
(2)求证:对于给定的正整数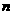 (
(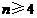 ),存在一个各项及公差均不为零的等差数列
),存在一个各项及公差均不为零的等差数列


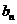 ,其中任意三项(按原来的顺序)都不能组成等比数列.
,其中任意三项(按原来的顺序)都不能组成等比数列.
38. 设数列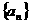 是公差为
是公差为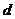 ,且首项为
,且首项为 的等差数列,
的等差数列,
求和: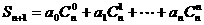
37.将等差数列{ }的所有项依次排列,并如下分组:(
}的所有项依次排列,并如下分组:( ),(
),(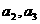 ),(
),( ),…,其中第1组有1项,第2组有2项,第3组有4项,…,第n组有
),…,其中第1组有1项,第2组有2项,第3组有4项,…,第n组有 项,记Tn为第n组中各项的和,已知T3=-48,T4=0,
项,记Tn为第n组中各项的和,已知T3=-48,T4=0,
(I)求数列{ }的通项公式;
}的通项公式;
(II)求数列{Tn}的通项公式;
(III)设数列{ Tn }的前n项和为Sn,求S8的值.
36.数列{ }的前n项和为
}的前n项和为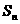 ,且满足
,且满足
(I)求 与
与 的关系式,并求{
的关系式,并求{ }的通项公式;
}的通项公式;
(II)求和
35.设数列{ }中,
}中, 中5的倍数的项依次记为
中5的倍数的项依次记为
 ,
,
(I)求 的值.
的值.
(II)用k表示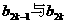 ,并说明理由.
,并说明理由.
(III)求和: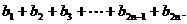
34.已知数列{ }满足:
}满足: 的前n项和
的前n项和
 .
.
33.已知数列{ }的各项分别为
}的各项分别为 的前n项和
的前n项和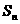 .
.
32. 已知数列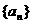 的各项为正数,其前n项和
的各项为正数,其前n项和 ,
,
(I)求 之间的关系式,并求
之间的关系式,并求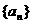 的通项公式;
的通项公式;
(II)求证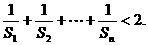
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com