
题目列表(包括答案和解析)
3.已知双曲线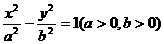 的离心率为
的离心率为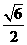 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
A.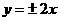 B.
B.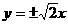 C.
C.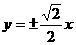 D.
D.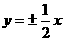
2.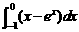 =
=
A.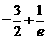 B.–1 C.
B.–1 C.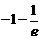 D.
D.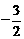
1.已知
A.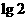 B.
B.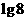 C.
C.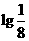 D.
D.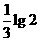
20.(本小题满分13分)
解:(Ⅰ)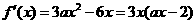 .
.
因为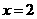 是函数
是函数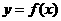 的极值点,所以
的极值点,所以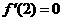 ,即
,即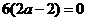 ,
,
所以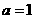 .经检验,当
.经检验,当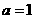 时,
时,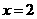 是函数
是函数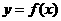 的极值点.
的极值点.
即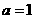 .
…………………6分
.
…………………6分
(Ⅱ)由题设,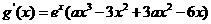 ,又
,又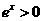 ,
,
所以,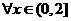 ,
,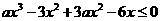 ,
,
这等价于,不等式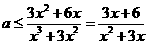 对
对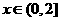 恒成立.
恒成立.
令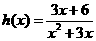 (
(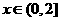 ),
),
则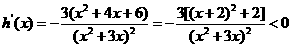 ,
,
所以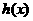 在区间
在区间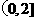 上是减函数,
上是减函数,
所以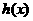 的最小值为
的最小值为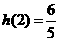 .
.
所以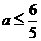 .即实数
.即实数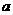 的取值范围为
的取值范围为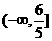 . …………………13分
. …………………13分
注:其他解法相应给分
19.(本题满分14分)
解:(Ⅰ)由题意可得点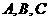 的坐标分别为
的坐标分别为 .
.
设椭圆的标准方程是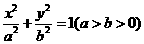 .
.
则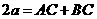 ,
,
即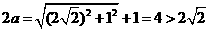 ,所以
,所以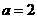 .
.
所以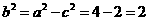 .
.
所以椭圆的标准方程是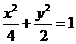 .7分
.7分
(Ⅱ) 由题意知,直线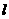 的斜率存在,可设直线
的斜率存在,可设直线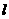 的方程为
的方程为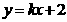 .
.
由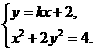 得
得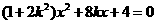 .
.
因为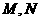 在椭圆上,
在椭圆上,
所以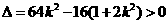 .
.
设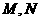 两点坐标分别为
两点坐标分别为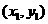 ,
,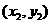 .
.
则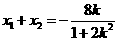
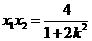 ,
,
若以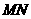 为直径的圆恰好过原点,则
为直径的圆恰好过原点,则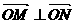 ,
,
所以
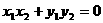 ,
,
所以,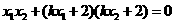 ,
,
即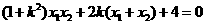 ,
,
所以,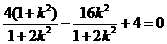 , 即
, 即 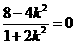 ,
,
得
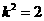 ,
,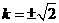
经验证,此时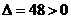 .
.
所以直线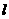 的方程为
的方程为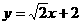 ,或
,或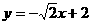 .
.
即所求直线存在,其方程为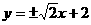 .
…………………14分
.
…………………14分
18.(本小题满分13分)
解:(I)由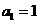 ,及
,及 ,
,
得 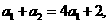
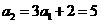 ,所以
,所以 .
.
由  ,
①
,
①
则当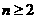 时,有
时,有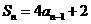 , ②
, ②
②-① 得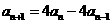 ,所以
,所以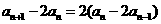 ,
,
又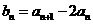 ,所以
,所以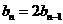 ,所以
,所以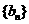 是以
是以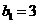 为首项、以
为首项、以 为公比的等比数列.
…………………6分
为公比的等比数列.
…………………6分
(II)由(I)可得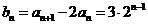 ,所以
,所以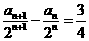 .
.
所以 数列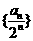 是首项为
是首项为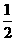 ,公差为
,公差为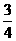 的等差数列.
的等差数列.
所以 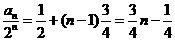 ,即
,即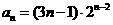 (
(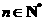 ).…………13分
).…………13分
17.(本小题满分13分)
解:(Ⅰ)设矩形的另一边长为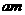 ,
,
则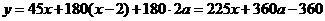 .
.
由已知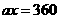 ,得
,得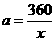 ,
,
所以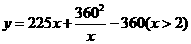 . …………………………6分
. …………………………6分
(II)因为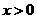 ,所以
,所以 ,
,
所以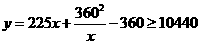 ,当且仅当
,当且仅当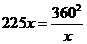 时,等号成立.
时,等号成立.
……………………12分
即当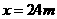 时,修建围墙的总费用最小,最小总费用是
时,修建围墙的总费用最小,最小总费用是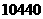 元.…………13分
元.…………13分
16.(本小题满分14分)
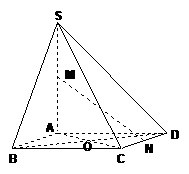
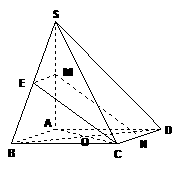 (Ⅰ)证明:如图,取
(Ⅰ)证明:如图,取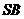 中点
中点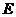 ,连结
,连结 、
、 ,
,
因为 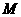 为
为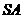 的中点,
的中点,
所以  ∥
∥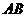 ,且
,且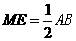 ,
,
因为 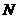 为
为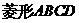 边
边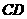 的中点,
的中点,
所以  且
且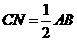 ,
,
所以 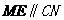 ,且
,且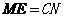 ,
,
所以 四边形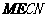 是平行四边形,
是平行四边形,
所以 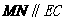 ,
,
又因为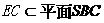 ,
,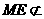 平面
平面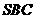 ,
,
所以直线 .
……………………………5分
.
……………………………5分
(Ⅱ)证明:如图,连结 ,相交于点
,相交于点 ,
,
因为 ,
,
 所以
所以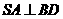 .
.
因为四边形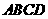 是菱形,
是菱形,
所以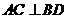 .
.
又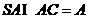 ,
,
所以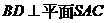 .
.
又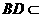 平面
平面 ,
,
所以平面
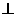 平面
平面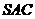 .
……………………………10分
.
……………………………10分
(Ⅲ)解:如图,连结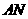 ,因为
,因为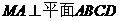 ,
,
所以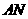 是
是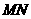 在平面
在平面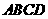 上的射影,
上的射影,
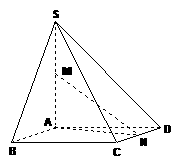 所以
所以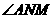 是直线
是直线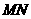 与平面
与平面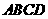 所成的角.
所成的角.
设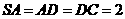 ,
,
由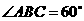 ,
,
可知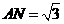 ,
, ,
,
所以在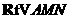 中
中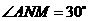 ,
,
即直线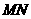 与平面
与平面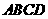 所成的角为
所成的角为 . ……………………………14分
. ……………………………14分
也可用空间向量来解决本题(略)
15.(本小题满分13分)
解:(Ⅰ)根据三角函数的定义,得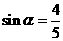 ,
,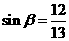 .
.
又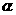 是锐角,所以,
是锐角,所以,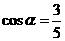 .……………………………4分
.……………………………4分
(Ⅱ)由(Ⅰ)知,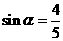 ,
,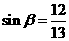 .
.
又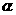 是锐角,
是锐角,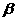 是钝角,
是钝角,
所以 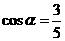 ,
,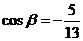 .
.
所以 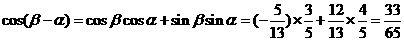 .……9分
.……9分
(Ⅲ)由题意可知,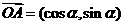 ,
,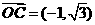 .
.
所以
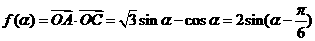 ,
,
因为 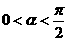 ,所以
,所以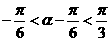 ,
,
所以函数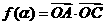 的值域为
的值域为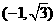 .……………………………13分
.……………………………13分
9. 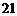 ,
,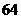 10.②和④ 11.
10.②和④ 11.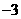 12.
12.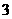 ,
,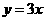 13.
13. 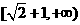 14.
14. 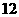
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com