10．(2008·湖南高考)已知函数f(x)＝(a≠1)．

(1)若a>0，则f(x)的定义域是________；

(2)若f(x)在区间(0,1]上是减函数，则实数a的取值范围是________．

解析：(1)∵a>0且a≠1，要使f(x)有意义，只需3－ax≥0，即x≤.

∴x∈；

(2)若a＝0，f(x)＝－不合题意；

若a<0，y＝是(0,1]上的增函数，且a－1<0，

∴f(x)是(0,1]上的减函数；

若a>0，∵y＝是(0,1]上的减函数，故需a－1>0，∴a>1，另一方面，f(x)的定义域为，

∴≥1，∴a≤3，∴a∈(1,3]．　

综上知a∈(－∞，0)∪(1,3]．

答案：(1)　(2)(－∞，0)∪(1,3]

9．若函数f(x)＝log_a(2x²+x)(a>0，a≠1)在区间(0，)内恒有f(x)>0，则f(x)的单调递增区间为__________．

解析：当x∈(0，)时，0<2x²+x<1，又f(x)>0，则0<a<1.

由2x²+x>0，解得：x<－或x>0，则f(x)的递增区间为(－∞，－)．

答案：(－∞，－)

8．函数y＝－(x－3)|x|的递增区间是__________．

解析：y＝－(x－3)|x|＝

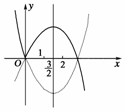
图1

作出该函数的图象，观察图象知递增区间为.

答案：

7．函数y＝ln的单调递增区间是__________．

解析：本题考查复合函数单调区间的确定；据题意需>0即函数定义域为(－1,1)，原函数的递增区间即为函数u(x)＝在(－1,1)上的递增区间，由于u′(x)＝()′＝>0.故函数u(x)＝在(－1,1)上的递增区间即为原函数的递增区间．

答案：(－1,1)

6．(2010·河南六市一模)奇函数f(x)在区间(－∞，0)上单调递减，f(2)＝0，则不等式(x－1)f(x+1)>0的解集为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(－2，－1)∪(1,2)　 　　　　　　　　　　　　　 B．(－3,1)∪(2，+∞)

C．(－3，－1)　 　　　　　　　　　　　　　　　　　　 D．(－2,0)∪(2，+∞)

解析：奇函数f(x)在区间(－∞，0)上单调递减，在区间

(0，+∞)上单调递减，由f(2)＝0得f(－2)＝0，则不等式

(x－1)f(x+1)>0，即

或

其解集为(－3，－1)，故选C.

答案：C

5．设f(x)是定义在R上以2为周期的偶函数，已知x∈(0,1)时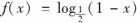，，则函数f(x)在(1,2)上　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　

(　)

A．是增函数，且f(x)<0　 　　　　　　　　　　　　 　　B．是增函数，且f(x)>0

C．是减函数，且f(x)<0　 　　　　　　　　　　　　 　　D．是减函数，且f(x)>0

解析：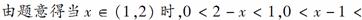

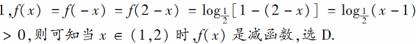
答案：D

4．已知f(x)＝log_a[(3－a)x－a]是其定义域上的增函数，那么a的取值范围是(　)

A．(0,1)　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．(1,3)

C．(0,1)∪(1,3)　 　　　　　　　　　　　　　　　　　　　　　 D．(3，+∞)

解析：由题知，或，解得1<a<3.故选B.

答案：B

3．函数y＝log_a(x²+2x－3)，当x＝2时y>0，则此函数的单调递减区间是　　　　　 (　)

A．(－∞，－3)　 　　　　　　　　　　　　　　　　　　　　　　　　 B．(1，+∞)

C．(－∞，－1)　 　　　　　　　　　　　　　　　　　　　　　 D．(－1，+∞)

解析：当x＝2时，y＝log_a5>0，

∴a>1，

由x²+2x－3>0⇒x<－3或x>1，

易见函数t＝x²+2x－3在(－∞，－3)上递减，　

故函数y＝log_a(x²+2x－3)(其中a>1)也在(－∞，－3)上递减．

答案：A

2．(2009·辽宁高考)已知偶函数f(x)在区间[0，+∞)上单调增加，则满足f(2x－1)<f的x的取值范围是　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A. 　　　 　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：f(x)是偶函数，其图象关于y轴对称，又f(x)在

[0，+∞)上递增，∴f(2x－1)<f⇔|2x－1|<⇔<x<.故选A.

答案：A

1．(2009·福建高考)下列函数f(x)中，满足“对任意x₁，x₂∈(0，+∞)，当x₁<x₂时，都有f(x₁)>f(x₂)”的是　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．f(x)＝　　　　　　　　　　　　　　　　　　　 B．f(x)＝(x－1)²

C．f(x)＝e^x　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．f(x)＝ln(x+1)

解析：∵对任意的x₁，x₂∈(0，+∞)，当x₁<x₂时，都有f(x₁)>f(x₂)，∴f(x)在(0，+∞)上为减函数．故选A.

答案：A