7.函数y=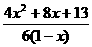(x>-1)的最小值是(　　 )

A.1　　　　　　　　　　 B.2　　　　　　　　　　 C.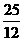　　　　　　　　 D.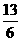

答案：B

解析：y=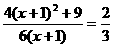(x+1)+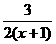≥2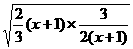=2(当且仅当x=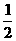时等号成立).

6.(2010天津河西区一模，8)若函数y=log₁₂(2-log₂x)的值域是(-∞,0),那么它的定义域是(　　 )

A.(0，2)　　　　　　　 B.(2，4)　　　　 C.(0，4)　　　　　　 D.(0，1)

答案：A

解析：∵y=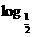(2-log₂x)的值域是(-∞，0)，

由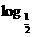(2-log₂x)<0,得2-log₂x>1.

∴log₂x<1.∴0<x<2.

故选择A.

5.值域是(0，+∞)的函数是(　　 )

A.y=x²-x+1　　　　　　　　　　　　　　　　 B.y=(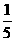)^1-x

C.y=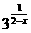+1　　　　　　　　　　　　　　　　 D.y=|log₂x²|

答案：B

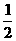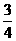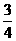解析：∵y=x²-x+1=(x-)²+≥，y=(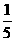)^1-x>0,

y=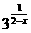+1>1且y≠2,

y=|log₂x²|≥0.

4.函数y=log_0.5(x+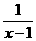+1)(x>1)的值域是(　　 )

A.(-∞,2]　　　　　　 B.(-∞,-2]　　　　　 C.［2,+∞)　　　　　 D.［-2,+∞)

答案：B

解析：∵x>1,∴x+1x-1+1=(x-1)+1x-1+2≥2+2=4.

∴log_0.5(x+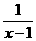+1)≤log_0.54=-2,?∴y∈(-∞，-2］.

3.函数y=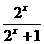的值域是(　　 )

A.(0,3]　　　　　　　　　　　　　　　　　　 B.(0,1)

C.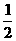［,+∞)　　　　　　　　　　　　　　　　　 D.(-∞,2)∪(2,+∞)

答案：B

解析：∵y=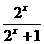=1-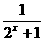,又2^x>0,∴2^x+1>1,-1<-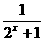<0.∴y∈(0,1).

2.函数y=lg(3-2x-x²)的值域是(　　 )

A.(-∞,1]　　　　　　　 B.［0,4］　　　　　　 C.(-∞，lg4]　　　　 D.［lg4,+∞)

答案：C

解析：∵3-2x-x²=-(x+1)²+4≤4,∴lg(3-2x-x²)≤lg4.

1.函数y=3-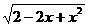的值域是(　　 )

A.(-∞,2)　　　　　　　 B.［1，2］　　　　　 C.［1，3］　　　　　　 D.［2，+∞)

答案：A

解析：y=3-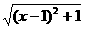,当x=1时，y_max=2.又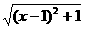在［1，+∞)中是增函数，因此y无最小值，故y∈(-∞,2］.

14.已知f(x)是定义在R上的不恒为零的函数，且对于任意的a、b∈R都满足f(a·b)=af(b)+bf(a).

(1)求f(0)、f(1)的值；

(2)判断f(x)的奇偶性，并证明你的结论.

解析：(1)f(0)=f(0·0)=0·f(0)+0·f(0)=0,

由f(1)=f(1·1)=1·f(1)+1·f(1),得f(1)=0.

(2)f(x)是奇函数.

证明：因为f(1)=f［(-1)²］=-f(-1)-f(-1)=0,

所以f(-1)=0,f(-x)=f(-1·x)=-f(x)+xf(-1)=-f(x).因此,f(x)为奇函数.

13.如果偶函数f(x)在x∈［0，+∞］上是增函数，且f(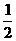)=0,求不等式f(log_ax)>0(0<a≠1)的解集.

解析：∵f(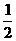)=0,∴f(log_ax)>f().

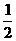∵偶函数f(x)在x∈［0，+∞］上是增函数,

∴f(|log_ax|)>f(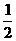),∴|log_ax|>.

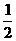即log_ax>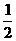或log_ax<-.

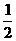①当0<a<1时，0<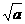x<或x>;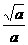

②当a>1时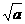,x>或0<x<.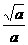

12.设f(x)是定义在R上的偶函数，其图象关于直线x=1对称，对任意x₁,x₂∈［0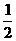，］都有f(x₁+x₂)=f(x₁)·f(x₂).

(1)设f(1)=2,求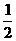f(),f();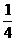

(2)证明f(x)是周期函数.

(1)解析：令x₁=x₂=.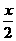

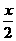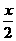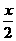则f(x)=f(+)=f²()≥0.

再令x₁=x₂=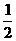,∴f(1)=f²().

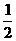∴f()=；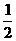

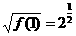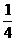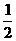令x₁=x₂=,∴f()=f²().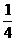

∴f()=.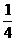

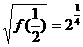(2)证明：∵f(x)是偶函数，∴f(-x)=f(x).

又因f(x)的图象关于直线x=1对称，

∴f(x+2)=f(-x),

∴f(x+2)=f(x).

即f(x)是周期为2的周期函数.