
题目列表(包括答案和解析)
4. 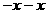 合并同类项得( )
合并同类项得( )
A. 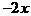 B.
0 C.
B.
0 C.
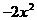 D.
D.
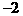
3. 下列说法正确的是( )
A. 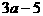 的项是
的项是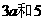 B.
B.
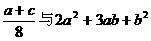 是多项式
是多项式
C. 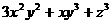 是三次多项式 D.
是三次多项式 D.
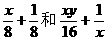 都是整式
都是整式
2. 下列式子中,二次三项式是( )
A. 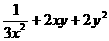 B.
B.
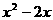
C. 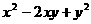 D.
D.
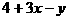
1. 下列整式中,不是同类项的是( )
A. 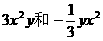 B.
1与-2
B.
1与-2
C. 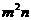 与
与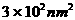 D.
D.
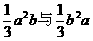
44.有一个两位数,它的十位上的数字比个位上的数字小3,十位上的数字与个位上的数字之和等于这个两位数的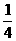 ,求这个两位数。
,求这个两位数。
3. 解:设甲数的个位数字为x,乙数的个位数字为y
则
解之可得
所以这两个数字为24和18
42三位数的数字之和是17,百位上的数字与十位上的数字的和比个位上的数大3,如把百位上的数字与个位上的数字对调,所得的新数比原数大495,求原数.

未知数,即各个数位上的数字.
题中有三个等量关系:
①三个数字之和等于17;
②百位数字与十位数字的和再与个位数字的差是3;
③调换后新数与原数之差是495.
(由学生自己设未知数,列方程组,求答案.教师提问一学生并板演解题过程)
解:设这个三位数的百位数字,十位数字,个位数字分别是x,y,z.依题意,得

解这个方程组,得

答:这个三位数是287.
43.数,甲数在20和30之间,乙数在10和20之间,甲、乙两数之比为4:3,如果甲、乙两数的个位数字与十位数字交换位置,这两个数之和为123,求甲、乙两数。
41、在等腰三角形中,一个角是另一个角的2倍,求三个角?_______________________
42:在等腰三角形中,一个边另一个边2倍,求三个边?_______________________
35、B两地相距5公里,一辆汽车与一辆自行车同时从A地出发,驶向B地,当汽车到达B地时,自行车才走完全程的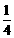 。汽车在B停留半小时后,以原速度返回A地,经过24分钟与自行车相遇。求汽车、自行车的速度。
。汽车在B停留半小时后,以原速度返回A地,经过24分钟与自行车相遇。求汽车、自行车的速度。
分析:根据在汽车到达B地时自行车才走完全程的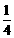 ,得到汽车的速度是自行车的速度的4倍。剩下
,得到汽车的速度是自行车的速度的4倍。剩下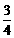 的路程,等于自行车行驶半小时加24分钟所走过的距离加上汽车行驶24分钟走过的距离。A、B之间的路程全长是已知的,只需设自行车和汽车的速度分别为x公里/小时,y公里/小时,就可列出方程。
的路程,等于自行车行驶半小时加24分钟所走过的距离加上汽车行驶24分钟走过的距离。A、B之间的路程全长是已知的,只需设自行车和汽车的速度分别为x公里/小时,y公里/小时,就可列出方程。
解:设自行车的速度为x公里/小时。
汽车的速度为y公里/小时。
依题意列方程组: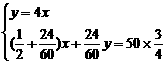
解此方程组得: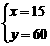
答:自行车速度为15公里/小时,汽车速度为60里/小时。
36辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能超过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?
37少先队夏令营到学校,先下山再走平路,一少先队员骑自行车以每小时12公里的速度
下山,以每小时9公里的速度通过平路,到学校共用了55分钟,回来时,通过平路速度不
变,但以每小时6公里的速度上山,回到营地共花去了1小时10分钟,问夏令营到学校有
多少公里?
分析:路程分为两段,平路和坡路,来回路程不变,只是上山和下山的转变导致时间的不
同,所以设平路长为x公里,坡路长为y公里,表示时间,利用两个不同的过程列
两个方程,组成方程组
解:设平路长为x公里,坡路长为y公里
依题意列方程组得: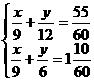
解这个方程组得: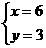
经检验,符合题意
x+y=9
答:夏令营到学校有9公里
38一列快车长168米,一列慢车长184米,如果两车相向而行,从相遇到离开需4秒,如果同向而行,从快车追及慢车到离开需16秒钟,求两车的速度。
分析:如果两车相向而行,则其相对速度为速度之和,如果两车同向而行,则其相对速度为速度之差,但是相对移动的距离则均为两辆火车的长度之和。
解:设快车时速为x公里/小时,慢车时速为y公里/小时,据分析可以得到方程组
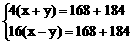
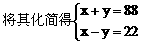

答:快车每小时行驶55公里,慢车每小时行驶33公里。
39余的两个角的比是2:3,求这两个角各是多少度?
分析:两角互余,和为90° 。解:设互余的两个角分别为2x°和3x°。 2x+3x=90°
x=18° 2x=36° 3x=54° 答:两角分别为36°,54°。
40个角的补角与它的余角的2倍的差是平角的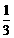 ,求这个角的度数。
,求这个角的度数。
分析:设这个角为x°,则这个角的补角为(180°-x°),这个角的余角为(90°-x°)
解:设这个设为x°,则
(180°-x)-2(90°-x)=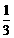 ×180°
×180°
x=60°
答:这个角为60°。
33.两地之间的路程为20千米,甲从A地,乙从B地同时出发,相向而行,2小时侯在C点相遇,相遇后甲原速反回A地,乙仍向A地前进。甲回到A地时,乙离A地还有2千米,求甲乙两地的时速。
学生活动:独立分析、思考、找相等关系,一个学生板演。
解:设甲速为每小时x千米,乙速为每小时y千米,根据题意,
 2(x+y)=20 ①
2(x+y)=20 ①
2x-2y=2 ②
解得
 x=5.5
x=5.5
y=4.5
答:甲速为每小时5.5千米,乙速为每小时4.5千米。
甲、乙二人从C点同向而行,甲回到A地的时间是2小时,在相同的时间内,乙到达D点,距A地还有2千米,从而可得相等关系:
甲行程-以行程=2千米
34乙两人由上午8时自A、B两地同时相向而行,上午10时相距36公里,两人继续前进,到12时又相距36公里,已知甲每小时比乙多走2公里,求A、B两地距离。(108公里)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com