
题目列表(包括答案和解析)
4. 求函数 y=x12+x22+…+xn2在x1+x2+…+xn=1的条件下的最小值。
3.
设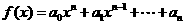 是n次的整系数多项式,a0,
an ,f(1) 都是奇数,则方程没有有理数根.
是n次的整系数多项式,a0,
an ,f(1) 都是奇数,则方程没有有理数根.
2. 求有理数a,b,c,使a,b,c是方程 x3+ax2+bx+c=0的三个根。
1.
求证:除m=n=p=0以外,不存在整数m,n,p,使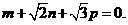
6. 设n为自然数,试求一个二次方程,它的两个解是二次方程 x2+2(n+1)x+6n-5=0的两个实数解的整数部分(所谓一个实数的整数部分,是指不超过此实数的最小整数)。
5.如果a与b都是整数,a<b, p自然数。
(1) 求在a与b之间分母为p的所有不是整数的分数之和S。
(2)
试证,S整数的的充分且必要条件是,(-1)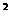 =(-1)
=(-1)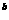 或者(-1)
或者(-1)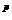 =-1.
=-1.
4.对整系数的二次函数f(n)=x2+ax+b,方程 f(x)=0 的解α与β满足不等式α>1,-1<β<1.
(1)写出a与b满足的不等式;
(2)当a固定时,在(1)的关系满足时,求使α为最小时的b,把它用a表示出来;
(3)在(1)的关系满足时求使α为最小时的a与b的值,并求此α的最小值。
3.对正整数n,设使方程2x2+2nx+m=0有实数解的正整数 m,一共有 a0个,试就 n为偶数和奇数两种情况,写出 an的表达式;并对偶数 N,求 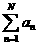 。
。
2. 设方程 y=x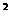 -(ab-a+b-1) x
-(ab-a+b-1) x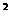 +(a
+(a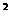 +ab+a)x-2 a
+ab+a)x-2 a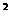 +1的图象对任何实数a均通过一定点,试求b的值以及定点的坐标。
+1的图象对任何实数a均通过一定点,试求b的值以及定点的坐标。
1、
设a , b 为有理数,已知A=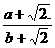 ,B=(a+
,B=(a+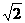 )(b+
)(b+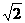 ),
),
满足B=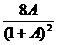 的关系,试根据“
的关系,试根据“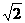 为无理数”,a与b的关系。
为无理数”,a与b的关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com