3、在平面内有n条两两不平行的直线，并过其中任意两条直线的交点还有一条已知直线。求证：这n条直线都通过同一个点。

2、如图所示，有一个正方体形的铁丝架，把它的侧棱

中点I、J、K、L也用铁丝连上。

(1)现在一个蚂蚁想沿着铁丝从A点爬到G点，问最

近的路线一共有几条？并用字母把这些路线表示出来(用所

经过的连结点字母表示，譬如蚂蚁从A点出发，经过I点、

L点，最后到达H点，这样的路线用AILH表示)。

(2)蚂蚁是否可能从A点出发，沿着铁丝经过每一个连结点恰好一次，最后到达G点？如果可能，请找出一条这样的路线；如果不可能，说明为什么？

1、圆周上有12个点，其中有一个点涂了红色，还有一个点涂了蓝色，其余10个点没有涂色，以这些点为顶点的凸多边形中，其顶点包含了红点及蓝点的多边形称双色多边形，只包含红点(蓝点)的称红色(蓝色)多边形，不包含红点及蓝点的称无色多边形。

试问：以这12个点为顶的所有凸多边形(边数可以从三角形到12边形)中，双色多边形的个数与无色多边形的个数，哪种多？多多少个？

3. 求使得不等式| x²+px+q |≤z, 当1≤x ≤5时恒成立的实数对(p, q).

2. 试求出所有的整数k, 使得x的一元二次方程 kx²－2(3k－1)x+9k－1=0 的某一根是一个分母为1999的既约分数.

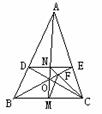
1. 如图, 在△ABC中, DE∥BC, 且DE=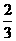BC, BE与CD相交于点O, AO与BC、DE分别交于点M、N, CN与BE交于点F, 连结FM, 求证: FM= 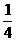AB.

10. 设M、N分别是△ABC两边AB、AC的中点, P是MN上任意一点,延长BP交AC于点Q, 延长CP交AB于R, 则= ________.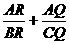

第 二 试

9. 在 △ABC中, ∠C = 90° , ∠A 的平分线AD交BC于D, 则 = _________.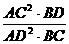

8. 等腰Rt△ABC中, D为斜边AB的中点, E、F分别为腰AC、BC上(并于端点)的点, DE⊥DF, AB=10, 设x=DE+DF, 则x的取值范围为______.

7. 正方形ABCD的边长为a, E是DC上一点, DE的长为b,　 AE的中垂线与AD、AE、BC分别交于P、M、Q, 则PM:MQ= 　　　　　　　.