
题目列表(包括答案和解析)
1、解简单高次方程的基本思路是 ,具体方法有:⑴因式分解法;⑵ .
14. (600+200)÷10=80(秒)
答:从车头进入隧道到车尾离开隧道共需80秒.
13. 288÷8-120÷60=36-2=34(米/秒)
答:列车的速度是每秒34米.
12. 182÷(20-18)=91(秒)
11. 1034÷(20-18)=91(秒)
10. 要求过几分钟甲、乙二人相遇,就必须求出甲、乙二人这时的距离与他们速度的关系,而与此相关联的是火车的运动,只有通过火车的运动才能求出甲、乙二人的距离.火车的运行时间是已知的,因此必须求出其速度,至少应求出它和甲、乙二人的速度的比例关系.由于本问题较难,故分步详解如下:
①求出火车速度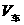 与甲、乙二人速度
与甲、乙二人速度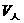 的关系,设火车车长为l,则:
的关系,设火车车长为l,则:
(i)火车开过甲身边用8秒钟,这个过程为追及问题:
故
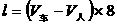 ;
(1)
;
(1)
(i i)火车开过乙身边用7秒钟,这个过程为相遇问题:
故
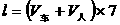 .
(2)
.
(2)
由(1)、(2)可得: 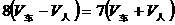 ,
,
所以,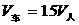 .
.
②火车头遇到甲处与火车遇到乙处之间的距离是:
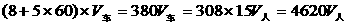 .
.
③求火车头遇到乙时甲、乙二人之间的距离.
火车头遇甲后,又经过(8+5×60)秒后,火车头才遇乙,所以,火车头遇到乙时,甲、乙二人之间的距离为:
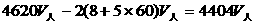
④求甲、乙二人过几分钟相遇?
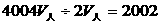 (秒)
(秒)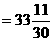 (分钟)
(分钟)
答:再过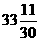 分钟甲乙二人相遇.
分钟甲乙二人相遇.
9. 这样想:列车越过人时,它们的路程差就是列车长.将路程差(90米)除以越过所用时间(10秒)就得到列车与人的速度差.这速度差加上人的步行速度就是列车的速度.
90÷10+2=9+2=11(米)
答:列车的速度是每秒种11米.
8. 解:从车头相遇到车尾离开,两车所行距离之和恰为两列车长之和,故用相遇问题得所求时间为:(120+60)¸(15+20)=8(秒).
7. 设火车车身长x米,甲、乙两人每秒各走y米,火车每秒行z米.根据题意,列方程组,得
|
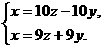
①-②,得: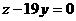
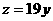
火车离开乙后两人相遇时间为:
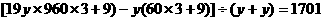 (秒)
(秒)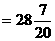 (分).
(分).
6. 设火车车身长x米,车身长y米.根据题意,得
|
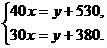
解得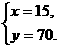
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com