
题目列表(包括答案和解析)
4.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或32 D.37 或 33
3.若等腰△ABC的腰长AB=2,顶角∠BAC=120°,以 BC为边的正方形面积为( )
A.3 B.12 C.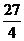 D.
D.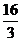
2.若△ABC的三边a、b、c满足a2+b2+c2十338=10a+24b+26c,则△ABC的面积是( )
A.338 B.24 C.26 D.30
1.三角形的三边长分别为 a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
1.B 2.A 3.B 4.C 5.C 6.C 7.C 8.C 9.C 10.B 11. 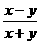 12.
12.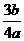 ,
,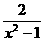 13.1 14.
13.1 14.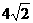 15.12 16.200
17.
15.12 16.200
17.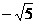 18.
18.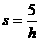 19.-2 20.
19.-2 20. 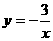 21.(1)
21.(1)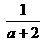 ;(2)
;(2)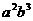 ;(3)
;(3)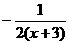 ;(4)
;(4)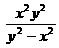 22.(1)
22.(1)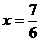 ;(2)
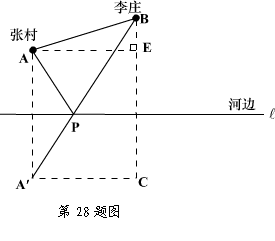
;(2)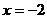 不是原方程的根,原方程无解 23.蜗牛神的速度是每小时6米,蚂蚁王的速度是每小时24米 24.1200米 25.先用勾股定理求出AC=2米,CE=1.5米,所以AE=0.5米 26.(1)m = ;(2)180 27.(1)B(3,3),k=9;(2)(,6),(6,);(3)S = 9- 或S = 9-3m 28.(1)作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置,此时,PA+PB的长度之和最短,即所铺设水管最短;(2)过B点作l的垂线,过A′作l的平行线,设这两线交于点C,则∠C=90°.又过A作AE⊥BC于E,依题意BE=5,AB=13,∴
AE2=AB2-BE2=132-52=144.∴ AE=12.由平移关系,A′C=AE=12,Rt△B A′C中,∵ BC=7+2=9,A′C=12,∴ A′B′=A′C2+BC2=92+122=225 , ∴ A′B=15.∵
PA=PA′,∴ PA+PB=A′B=15.∴
1500×15=22500(元)
不是原方程的根,原方程无解 23.蜗牛神的速度是每小时6米,蚂蚁王的速度是每小时24米 24.1200米 25.先用勾股定理求出AC=2米,CE=1.5米,所以AE=0.5米 26.(1)m = ;(2)180 27.(1)B(3,3),k=9;(2)(,6),(6,);(3)S = 9- 或S = 9-3m 28.(1)作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置,此时,PA+PB的长度之和最短,即所铺设水管最短;(2)过B点作l的垂线,过A′作l的平行线,设这两线交于点C,则∠C=90°.又过A作AE⊥BC于E,依题意BE=5,AB=13,∴
AE2=AB2-BE2=132-52=144.∴ AE=12.由平移关系,A′C=AE=12,Rt△B A′C中,∵ BC=7+2=9,A′C=12,∴ A′B′=A′C2+BC2=92+122=225 , ∴ A′B=15.∵
PA=PA′,∴ PA+PB=A′B=15.∴
1500×15=22500(元)
1.D 2.B 3.A 4.C 5.D 6.A 7.C 8.C 9.50
10.10
11.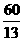 12.6,8,10 13.24 14.100mm 15.③ 16.
12.6,8,10 13.24 14.100mm 15.③ 16.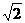 m 17.略 18.证
m 17.略 18.证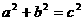 ,用勾股定理逆定理得∠C=90° 19. 设城门高为
,用勾股定理逆定理得∠C=90° 19. 设城门高为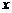 米,则竿长为
米,则竿长为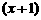 米,依题意,得
米,依题意,得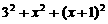 ,解得
,解得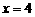 ,故竿长为5米 20. 如图,过点B作BC⊥AD于C,则AC=2.5,BC=6,由勾股定理求得AB=6.5(km) 21.5cm
22. 3.75尺 23.12海里/时 24.先由勾股定理求得AB=10cm,设DC=xcm,则DE=xcm,BD=(8-x)cm,BE=4cm,(8-x)2=x2+42,解得x=3(cm) 25.15km 26. 如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线. 在Rt△A′DB中,由勾股定理求得A′B=17km
,故竿长为5米 20. 如图,过点B作BC⊥AD于C,则AC=2.5,BC=6,由勾股定理求得AB=6.5(km) 21.5cm
22. 3.75尺 23.12海里/时 24.先由勾股定理求得AB=10cm,设DC=xcm,则DE=xcm,BD=(8-x)cm,BE=4cm,(8-x)2=x2+42,解得x=3(cm) 25.15km 26. 如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线. 在Rt△A′DB中,由勾股定理求得A′B=17km

期中综合测试
5.3或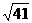 6.120cm2 7.由BD2+DC2=122+162=202=BC2得CD⊥AB又AC=AB=BD+AD=12+AD,在Rt△ADC中,AC2=AD2+DC2,即(12+AD)2=AD2+162,解得AD=
6.120cm2 7.由BD2+DC2=122+162=202=BC2得CD⊥AB又AC=AB=BD+AD=12+AD,在Rt△ADC中,AC2=AD2+DC2,即(12+AD)2=AD2+162,解得AD=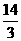 ,故 △ABC的周长为2AB+BC=
,故 △ABC的周长为2AB+BC=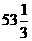 cm 8.由勾股定理的逆定理可判定△ABC是直角三角形,由面积关系可求出公路的最短距离BD=
cm 8.由勾股定理的逆定理可判定△ABC是直角三角形,由面积关系可求出公路的最短距离BD=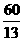 km, ∴最低造价为120000元 9.设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,∴(x+10)2+52=(15-x)2,解得x=2,∴10+x=12(米) 10.如图,将△APC绕点C旋转,使CA与CB重合,即△APC≌△BEC,∴△PCE为等腰Rt△,∴∠CPE=45°,PE2=PC2+CE2=8. 又∵PB2=1,BE2=9,∴PE2+ PB2= BE2,则∠BPE=90°,∴∠BPC=135°.
km, ∴最低造价为120000元 9.设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,∴(x+10)2+52=(15-x)2,解得x=2,∴10+x=12(米) 10.如图,将△APC绕点C旋转,使CA与CB重合,即△APC≌△BEC,∴△PCE为等腰Rt△,∴∠CPE=45°,PE2=PC2+CE2=8. 又∵PB2=1,BE2=9,∴PE2+ PB2= BE2,则∠BPE=90°,∴∠BPC=135°.

单元e线(十八)
1.B 2.D 3.C 4.5,12,13; 8,15,17; 11,60,61(此题答案不唯一)
18.2 勾股定理的逆定理(2)
1.B 2.A 3.B 4.C 5.C 6.24m2 7.符合 8.由勾股定理得AE2=25,EF2=5,AF2=20,∵AE2= EF2 +AF2,∴△AEF是直角三角形 . 9.略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com