
题目列表(包括答案和解析)
3.理解多边形的内角和与外角和定理:
(1)几边形:平面内n(n≥3)条线段首尾顺次相接,如果其中任何两条线段都不在同一直线上,所组成的图形叫做n边形.
(2)多边形内角和定理:n边形内角和等于(n-2)·180°,(n≥3,n为自然数)
(3)多边形外角和定理:n边形外角和等于360°(n≥3,n为自然数)
2.掌握四边形的内角和等于360°,外角和等于360°的性质;
1.理解四边形与四边形的边、顶点、内角、对角线等概念;
四边形:平面内,四条线段首尾顺次相接,如果任何两条线段都不在同一直线上,所形成的图形叫做四边形;
边:组成四边形各边的线段; 顶点:相邻两边的公共点; 内角:从四边形内部看相邻两边所成的角,简称为角;对角线:连结四边形不相邻的两个顶点的线段;外角:四边形的一条边与相邻边延长线组成的角;
4.利用因式分解进行计算:
(1)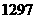 的
的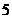 ﹪减去
﹪减去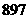 的
的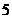 ﹪,差是多少?(2)
﹪,差是多少?(2)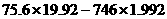
(3)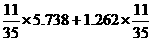 (4)
(4)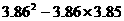 (5)
(5)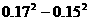
(6)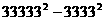 (7)
(7)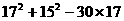 (8)
(8)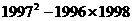
3.若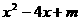 可分解成
可分解成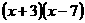 ,求
,求 的值;
的值;
2.若多项式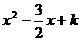 是一个完全平方式,求
是一个完全平方式,求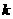 的值是多少?
的值是多少?
1.把下列各式分解因式:
(1)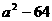 (2)
(2)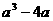 (3)
(3)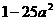 (4)
(4)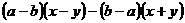
(5)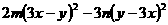 (6)
(6)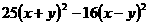 (7)
(7)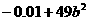
(8)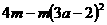 (9)
(9)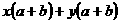 (10)
(10)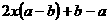
(11)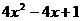 (12)
(12)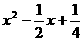 (13)
(13)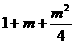
(14)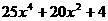 (15)
(15)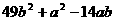 (16)
(16)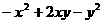
(17)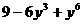 (18)
(18)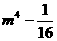
(19)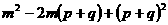 (20)
(20)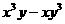 (21)
(21)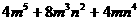
2.解答题:
(1) 已知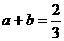 ,
,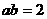 ,求
,求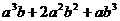 的值;
的值;
(2) 已知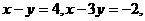 求
求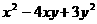 的值;
的值;
(3) 已知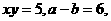 求
求
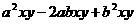 的值;
的值;
(4) 已知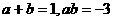 ,求
,求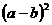 的值;
的值;
因式分解复习题:A组
1.把下列各式分解因式:
(1) 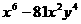 (2)
(2) 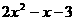 (3)
(3) 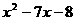 (4)
(4) 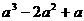
(5) 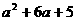 (6)
(6) 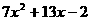 (7)
(7) 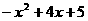 (8)
(8) 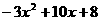
(9) 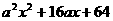 (10)
(10) 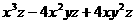 (11)
(11) 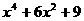
(12) 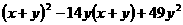 (13)
(13) 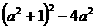 (14)
(14) 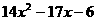
(15)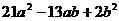 (16)
(16) 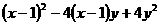 (17)
(17) 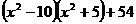
(18)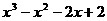 (19)
(19)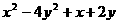 (20)
(20)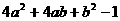
25.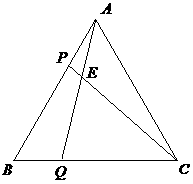 (12分)如图,等边三角形
(12分)如图,等边三角形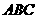 的边长为3,点
的边长为3,点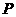 、
、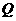 分别是
分别是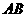 、
、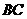 上的动点(点
上的动点(点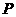 、
、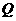 与三角形
与三角形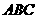 的顶点不重合),且
的顶点不重合),且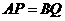 ,
, 、
、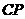 相交于点
相交于点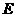 .
.
(1)如设线段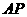 为
为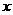 ,线段
,线段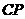 为
为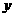 ,求
,求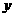 关于
关于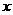 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(2)当△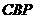 的面积是△
的面积是△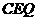 的面积的2倍时,求
的面积的2倍时,求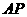 的长;
的长;
(3)点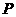 、
、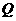 分别在
分别在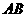 、
、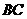 上移动过程中,
上移动过程中, 和
和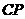 能否互相垂直?如能,请指出
能否互相垂直?如能,请指出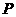 点的位置;如不能,请说明理由.
点的位置;如不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com