
题目列表(包括答案和解析)
1. (2005年玉林)已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB之比为 ( )
A.3:4 B.2:3 C.3:5 D.1:2
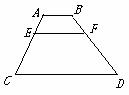
3.灵活运用平行线分线成比例定理,它的前提条件是知道有平行线的存在,然后得到了对应线段成比例,但反过来就不一定正确,如下左图,如果AB∥CD∥EF,可以得到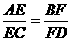 ,如下右图,如果
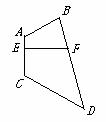
,如下右图,如果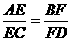 ,但不一定得到AB∥CD∥EF.
,但不一定得到AB∥CD∥EF.
[基础演练]
2.在判断给定的四条线段是否成比例,常用的方法是先将四条线段长度化成统一的单位,再按从小到大的顺序排列,将最长线段与最短线段的长度乘积与中间两条线段的长度乘积比较,如果积相等,则四条线段成比例;否则不成比例.如已知线段a、b、c、d,a=2厘米,b=30米,c=6厘米,d=10米,试判断它们是否为成比例线段?不要认为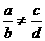 ,所以线段a、b、c、d不成比例,这样的方法是错误的.
,所以线段a、b、c、d不成比例,这样的方法是错误的.
1.灵活运用比例的基本性质,如例4中,知道了ac=bd,容易得到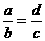 ,不会出现
,不会出现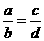 ,然后再利用
,然后再利用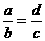 得到
得到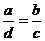 ,从而利用合比性质得到
,从而利用合比性质得到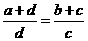 ;虽然得到
;虽然得到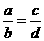 ,不会出现
,不会出现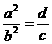 的结果的.
的结果的.
4.相似形的定义,如例4.
[典例精析]
例1:下列说法中正确的有 ( )
①两条线段的比是两条线段长度之比,比值是一个正数
②两条线段的长度比是“同一单位下”的长度比
③两条线段的比与所采用的长度单位无关
④两条线段的比有顺序,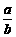 与
与 不同,它们互为倒数
不同,它们互为倒数
A.1个 B.2个 C.3个 D.4个
解析
两条线段的比,选用同一个长度单位量得两条线段的长度的比叫做两条线段的比.因为线段的长度都是正数,所以比值也是正数.又因为两条线段的比是一个没有单位的正数,因此与所采用的度量单位无关.两条线段a、b,除了a=b之外,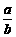 ≠
≠ ,所以两条线段的比是有顺序性的.四个说法都正确,故选D.
,所以两条线段的比是有顺序性的.四个说法都正确,故选D.
答案:D.
例2:已知点C把线段AB分成两条线段AC、BC,且AC>BC,下列说法错误的是( )
A.如果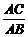 =
=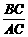 ,那么线段AB被点C黄金分割
,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C. AC与AB的比叫做黄金比
D. 0.618是黄金比的精确值
解析 点C为AB的黄金分割点,且AC>BC,则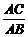 =
=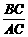 ,即AC2=AB·BC;反之,也成立.其中较长线段与原线段的比叫做黄金比.黄金比为
,即AC2=AB·BC;反之,也成立.其中较长线段与原线段的比叫做黄金比.黄金比为 ,约等于0.618.故选D. 答案:D
,约等于0.618.故选D. 答案:D
例3:已知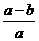 =
=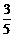 ,则
,则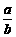 为 ( )
为 ( )
A. B.
B.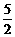 C.-
C.- D.-
D.-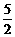
解析 由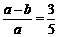 ,得5(a-b)=3a,所以2a=5b,得
,得5(a-b)=3a,所以2a=5b,得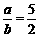 ,故选B.
,故选B.
答案:B.
例4:下面给出的图形中,不是相似的图形的是 ( )
A.刚买的一双手套的左右两只 B.仅仅宽度不同的两快长方形木板
C.一对羽毛球球拍 D.复印出来的两个“春”字
解析 仅仅宽度不同的两快长方形木板不一定是相似的.
答案:B.
例5:若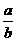 =
=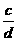 =
=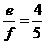 ,则
,则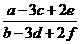 =____.
=____.
解析 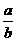 =
=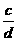 =
=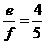 ,所以
,所以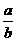 =
=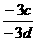 =
=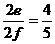 ,则
,则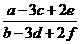 =
= . 答案:
. 答案: 例6:如图,l1∥l2∥l3,BC=3,
例6:如图,l1∥l2∥l3,BC=3,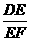 =2,则AB=___________.
=2,则AB=___________.
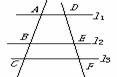
解析 运用平行线分线段成比例定理,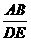 =
=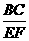 .
.
答案:6.
[常见误区]
3.平行线分线成比例定理的应用,如例6;
2.黄金分割的应用,如例2;
1.比例的性质,如例1、例3、例5;
3. 理解相似多边形的概念
3. 了解平行线分线成比例定理及截三角形两边或其延长线的直线平行于第三边的判定定理的证明,会用它们证明线段成比例、线段平行等问题,并会进行有关的计算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com