
题目列表(包括答案和解析)
2.若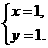 是方程组
是方程组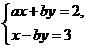 的解,则a,b的取值分别是( )
的解,则a,b的取值分别是( )
(A)-2,4 (B)5,2 (C)4,-2 (D)2,5
1.方程组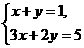 的解是( )
的解是( )
(A)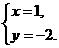 (B)
(B)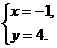 (C)
(C)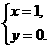 (D)
(D)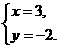
例1 (2004年北京市海淀区中考试题)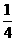 的平方根是_______,64的立方根是________.
的平方根是_______,64的立方根是________.
分析:由平方根和立方根的概念即可求得.
解: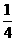 的平方根是±
的平方根是±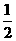 ,64的立方根是4.
,64的立方根是4.
例2 (2004年南京市中考试题)写出一个无理数,使它与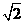 的积是有理数:____.
的积是有理数:____.
分析:这是一道开放题,只要符合题意即可.
解:-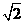 或
或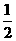
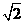 或3
或3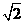 等等.
等等.
例3 (2003年江苏省南通市中考试题)给出下列程序:
输入x →立方 ×k→ +b→ 输出
且已知当输入的x值为1时,输出值为1;输入的x值为-1时,输出值为-3,则当输入的x值为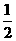 时,输出值为_____.
时,输出值为_____.
分析:按照程序图应有kx3+b=输出值,于是可根据题意可列出关于k,b的二元一次方程组,即可求得k,b.
解:设输出值为y,则有y=kx3+b.由条件,得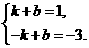 解得
解得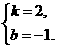 即y=2x3-1.
即y=2x3-1.
所以,当x=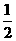 时,y=2×(
时,y=2×(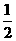 )3-1=
)3-1=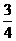 .
.
例4 (2003年湖北省孝感市中考题)已知方程组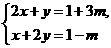 的解满足x+y<0,则m的取值范围是( ).
的解满足x+y<0,则m的取值范围是( ).
(A)m>-1 (B)m>1 (C)m<-1 (D)m<1
分析:常规解法可视m为已知,可求出关于x,y的二元一次方程组的解,再由x+y<0构造出不等式,即求出m的范围,但这道题目若将方程组的两式相加可直接求出x+y,从而可简捷求解.
解:将方程组的两式相加,得3(x+y)=2(1+m),即有x+y=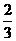 (1+m)<0,则m<-1,故应选C.
(1+m)<0,则m<-1,故应选C.
例5 (2004年哈尔滨市中考试题)“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,出厂价分别为:甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部,并将60000恰好用完,请你帮助商场计算一下如何购买.
分析:无论购进何种型号的手机,都有两个不变的量,计划将60000元钱全部用于购进其中两种不同型号的手机共40部,这样就可以利用60000元和40部这两个不变量列出方程组求解.不过题目中并没有指明选甲、乙、丙三种型号手机的哪两种,因此应分情况讨论.
解:设甲种型号手机要购买x部,乙种型号手机要购买y部,丙种型号手机要购买z部,根据题意,得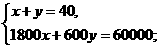 或
或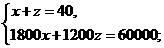 或
或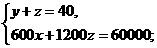
分别解这三个方程组,得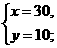 或
或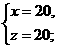 或
或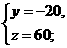 (不合题意,舍去)
(不合题意,舍去)
答:有两种购买方法:甲种型号手机购买30部,乙种型号手机购买10部;或甲种型号手机购买20部,丙种型号手机购买20部.
例6 (2004年重庆市北碚实验区中考试题)光明中学九年级甲、乙两班为“希望工程”捐款活动中,两班捐款的总数相同,均多于300元且少于400元.已知甲班有一人捐6元,其余每人都捐9元;乙班有一人捐13元,其余每人都捐8元,求甲、乙两班学生总数是多少人.
分析:若设甲班人数为x人,乙班人数为y人,则由两班捐款的总数相同和甲班有一人捐6元,其余每人都捐9元;乙班有一人捐13元,其余每人都捐8元,可无出一方程;由两班捐款均多于300元且少于400元,又可列出一个不等式,这样可以由人数是整数进行求解.
解:设甲班人数为x人,乙班人数为y人.
则根据题意,得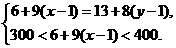
即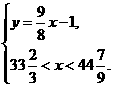
因为x是整数,所以x=34,35,36,37,38,39,40,41,42,43,44.
又因为y也是整数,所以x是8的倍数,即x=40,y=44,故x+y=84.
复习这三章应注意数学思想方法的运用,如在第八章“二元一次方程组”中,借助于平面直角坐标系,就可以用二元一次方程组的图象求得方程组的近似解,从而用几何的方法确定代数问题;在第九章“不等式与不等式组”中,用数轴表示不等式(组)的解集,体现了数形结合的思想;在第十章“实数”中,学习直线上的点与实数的一一对应以及平面上的点与有序实数对一一对应等,也体现了数形结合的思想.转化是数学中一种基本的也是非常重要的思想方法之一.如,在复习二元一次方程组的解法时,应注意体会二元化为一元的消元(转化)的思想.在列一次方程组解应用题和列不等式或不等式组解应用题,也应体会未知化为已知的转化思想.类比又是学习数学的一种有效方法.如,类比等式的性质得出不等式的性质,类比方程(组)的解法寻找不等式(组)的解法等.
(三)实数
1.平方根的性质:
(1)一个正数有两个平方根,它们互为相反数;
(2)0有一个平方根,它是0本身;
(3)负数没有平方根,正数的算术平方根是正数,0的算术平方根是0.求一个非负数的平方根的运算,叫做开平方.
开平方与平方是互逆运算,可以通过平方运算来求一个数的平方根,以及检验是不是另一个数的平方根.
2.如果一个数的立方等于a,那么这个数叫做a的立方根.正数有一个正的立方根,负数有一个负的立方根,0的立方根是0.求一个数的立方根的运算,叫做开立方.开立方与立方是互逆运算,任何数都有立方根,而负数没有平方根,这是开立方与开平方的重要区别.
3.有理数和无理数统称为实数,实数的分类可以从两个角度去思考.(请同学们进行思考)
4.实数和有理数一样也有许多重要的性质,可从以下几方面去思考:
(1)实数a的相反数是-a,具体地,若a与b互为相反数,则a+b=0;反之,若a+b=0,则a与b互为相反数;
(2)一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数,0的绝对值是0;
(3)乘积为1的两个实数互为倒数,即若a与b互为倒数,则ab=1;反之,若ab=1,则a与b互为倒数.这里应特别注意的是0没有倒数;
(4)实数与数轴上的点是一一对应的.也就是说所有的实数都可以用数轴上的点来表示;反之,数轴上的每一个点都表示一个实数;
(5)任意两个实数都可以比较大小;
(5)在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.
另外,有理数的运算律在实数范围内仍然适用.
(二)不等式与不等式组
1.表示大小关系的式子叫做不等式.含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.不等式有下列三个重要性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
2.解一元一次不等式与解一元一次方程基本相同,只是在化系数为1时注意不等式性质的运用,另外,不等式的最后结果是一个解集,确定不等式组的解集时应区分以下四种情况:
(1)同大取大;(2)同小取小;(3)大于小的,小于大的,取公共部分;(4)大于大的,小于小的,无解.
3.列不等式解应用题的基本方法与列一元一次方程解应用题的方法基本相同.
(一)二元一次方程组
1.含有两个未知数,并且未知数指数都是1的方程叫做二元一次方程.两个二元一次方程合在一起就组成了一个二元一次方程组.
2.解二元一次方程组的基本思路是消元,使之转化为一元一次方程,消元的方法有代入消元法和加减消元法.
3.列一次方程组解应用题的基本方法与列一元一次方程解应用题的方法相似.列一次方程组解应用题的常见题型有以下几种情形:
(1)和、差、倍、分问题,使两数和=较大的数+较小的数,较大的数=较小的数×倍数±增(或减)数;
(2)行程问题,即路程=速度×时间;
(3)工程问题,即工作量=工作效率×工作时间;
(4)浓度问题,即溶质质量=溶液质量×浓度;
(5)分配问题,即调配前后总量不变,调配后双方有新的倍比关系;
(6)等积问题,即变形前后的质量(或体积)不变;
(7)数学问题,即若个位的数字为a,十位上的数字为b,百位上的数字为c,则这三位数可表示为100c+10b+a,等等;
(8)经济问题,即利息=本金×利率×期数;本息和=本金+利息=本金+本金×利率×期数;税后利息=本金×利率×期数×(1-利息税率);商品的利润=商品的售价-商品的进价;商品的利率率=×100%;等等.
由于这部分知识都是研究数与代数的问题,均为基础内容,而且概念性又强,因而出现错误的频率很高,常见错误有以下几种:错误理解二元一次方程组解的概念;错误理解不等式和不等式组解集的概念;忽视对不等式性质的理解,特别是对性质3的运用;错解二元一次方程组和不等式及不等式组,如符号的错误,去括号的错误,去分母时漏乘的错误,移项的错误,忽视分数线的括号作用,解方程盲目代入,消元时没有目标;不等式的解集在数轴上表达错误;不等式组解集的表示错误;对算术平方根、平方根、立方根的理解错误;对无理数、实数概念的理解错误;另外列一次方程组和不等式(组)解应用题的错误等等.
纵观历年各地的中考试卷,都少不了这三章的知识,试题的题量和分值都约占全卷的10%左右,题型多为填空题、选择和解答题,试题的难度不大,少数省市将这部分知识渗透到其他知识中构建成综合题(压轴题).
4.会用计算器求正数的算术平方根和一个数的立方根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com