
题目列表(包括答案和解析)
4.
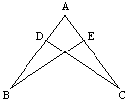
 如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______.
如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______.
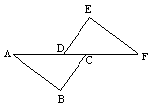
3. 已知:如图,△ABC≌△FED,且BC=DE.则∠A=__________,A D=_______.
2.如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________.
1.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边:_______.

3.3《全等三角形及其性质》同步练习
第1题. 你能沿虚线把下面图形划分成两个全等图形吗?请找出三种方法.
答案:
第2题. 你能把如图所示的一个三条边都相等的三角形分成两个全等的图形吗?能分成三个、四个、六个全等的图形吗?怎么分?

答案:
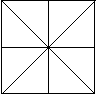
第3题. 你能把一个正方形分成八个全等的三角形吗?怎么分,请画出来.

答案:方法多种,答案不惟一.
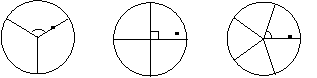
第4题. 你能把圆分成3个、4个、5个全等的图形吗?
答案:只需将圆心角(360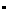 )3等分、4等分、5等分即可,如图所示
)3等分、4等分、5等分即可,如图所示
第5题. 在一个正方形的花园里,要怎样修建小路才能使这些小路正好把花园分成4个全等的三角形?如果要分成8个全等的三角形呢?
答案:
第6题. 你能把正方形分成2个、4个、8个全等的图形吗?
答案:分法可分别如下所示:

第7题. 在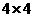 的方格纸上,沿着格线,把正方形划分为四个全等的图形,你可以得到几种不同的图形?
的方格纸上,沿着格线,把正方形划分为四个全等的图形,你可以得到几种不同的图形?
答案:每一种图形只能由4个小方格组成,考虑到 的限制,只能得到5种,如图所示:
的限制,只能得到5种,如图所示:
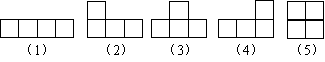
第8题. 找出下列图中的全等图形.

答案:根据全等形的定义得全等形有天鹅、荷花.
第9题. 你能把一个长方形分成两个全等的图形吗?怎么分?能分成三个全等的图形吗?若要分成四个、六个、八个、九个全等的图形,怎么分?
答案:能,如图所示

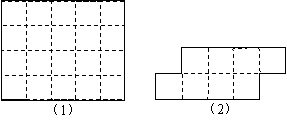
第10题.  图
图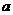 展示了沿网格可以将一个每边有4格的正方形分割成两个相同的部分.找出五种其他分割的方法.同样,你能将图
展示了沿网格可以将一个每边有4格的正方形分割成两个相同的部分.找出五种其他分割的方法.同样,你能将图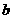 和图
和图 中的每一个图形分割成相同的两部分吗?
中的每一个图形分割成相同的两部分吗?
答案:
第11题. 你能把下边的矩形分成两个全等的三角形吗?能分成四个全等的三角形吗?

答案:(1)分成两个全等的三角形; (2)分成四个全等的三角形.


第12题. 请你说出实际生活中见到的全等图形的例子.
答案:答案不惟一,略.
第13题. 如图,正方形中有十二棵树,请你把这个正方形划分为四小块,要求每块的形状、大小都相同,并且每块中恰好有三棵树.

答案: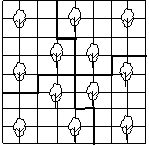
第14题. 走在马路上或是公园的小路上,你有没有发现地上铺的地砖有的虽然非常简单,却能拼出美丽的图案来?构成图案的每一块地砖都是全等的吗?你能否自己设计一种地砖,让每一块地砖都是全等的,而且能拼出美丽的图案?
答案:答案不惟一,略.
第15题. 将如图所示的小平行四边形的边 三等分,分点为
三等分,分点为 ,过
,过 作
作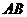 的平行线,交
的平行线,交 于点
于点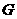 ,得多边形
,得多边形 ,请用四个这样的小多边形,拼成一个形状相同的大多边形.
,请用四个这样的小多边形,拼成一个形状相同的大多边形.

答案:
第16题. 仔细观察下图这幅由“箭头”组成的“风车”图案,你能说出它的绘制过程吗?请你动手做一做,更多的“箭头”会拼出怎样的图案?

答案:从一个菱形出发制作箭头,再拼成“风车”图案.
第17题. 按下列步骤设计图案:
(1)画一个正方形 ;
;
(2)去掉两个全等的直角三角形1,2;
(3)将直角三角形1,2分别放在3,4的位置上;
(4)在得到的图形上画上你喜欢的图案;
(5)再做出若干个这样的图案,利用它们拼出一个美丽的图案.
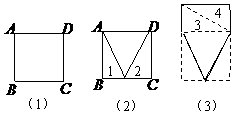
答案:答案不惟一,略.
第18题. 把一张方格纸贴在纸板上.按图1所示画上正方形,然后沿图示的直线切成5小块.当你照图2的样子把这些拼成正方形的时候中间居然出现了一个洞!
我们发现,图1的正方形是由49个小正方形组成的.图2中拼成的正方形却只有48个小正方形.哪一个小正方形没有了?它到哪去了?

答案: 5小块图形中最大的两块对换了位置之后,被那条对角线切开的每个小正方形都变得高比宽大一点点.这意味着这个大正方形不再是严格的正方形.它的高增加了,从而使得面积增加,所增加的面积恰好等于那个方洞的面积.
5小块图形中最大的两块对换了位置之后,被那条对角线切开的每个小正方形都变得高比宽大一点点.这意味着这个大正方形不再是严格的正方形.它的高增加了,从而使得面积增加,所增加的面积恰好等于那个方洞的面积.
第19题. 如图, ,且
,且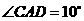 ,
, ,
,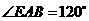 ,求
,求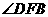 和
和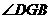 的度数.
的度数.

答案:因为 ,
,
所以
 .
.
所以
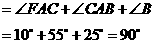

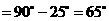 .
.
第20题. 如图所示,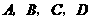 在同一直线上,且
在同一直线上,且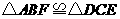 .求证:
.求证:

 .
.
答案:


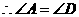
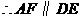 ;
;
又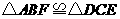

 ,
,
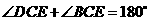
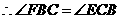
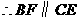 ;
;
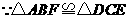
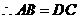
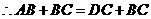 .即
.即 .
.
第21题. 长为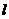 的两根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边
的两根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边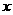 的取值范围为( )
的取值范围为( )
A. B.
B.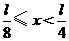 C.
C.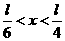 D.
D.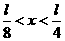
答案:当两全等三角形三边各自都相等时,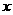 最小为
最小为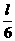 ,而每一个三角形周长为
,而每一个三角形周长为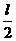 ,因此最长为
,因此最长为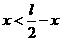 ,因此
,因此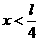 ,故选A.
,故选A.
第22题. 如图,点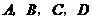 在一条直线上,△
在一条直线上,△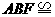 △
△ 你能得出哪些结论?
你能得出哪些结论?
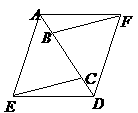
答案:由△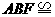 △
△ 可得到
可得到
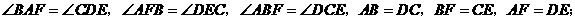
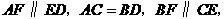 △
△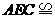 △
△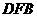 等.
等.
第23题. 如图,△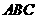 是一个钢架,
是一个钢架, 是连接点
是连接点 与
与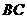 中点
中点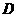 的支架,
的支架, 与
与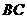 之间存在什么关系?小明的思考过程如下
之间存在什么关系?小明的思考过程如下

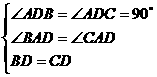
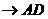 是
是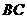 边上的中线、高线,也是
边上的中线、高线,也是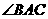 的角平分线.
的角平分线.
你能说明每一步的理由吗?

答案: 是
是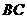 边上的中线、高线,也是
边上的中线、高线,也是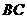 所对角的角平分线.
所对角的角平分线.
第一步:由“边边边”判定条件知两三角形全等;
第二步:全等三角形的对应角相等,对应边相等;
第三步:由中线、高线、角平分线的定义可得结论.
第24题. 如图所示, ,
,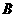 与
与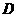 ,
,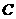 与
与 是对应点.
是对应点.
求证: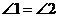 .
.
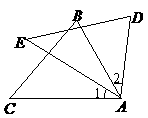
答案: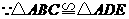

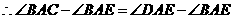 ,即
,即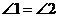 .
.
第25题. 如图所示,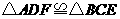 ,
,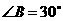 ,
,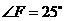 ,
,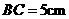 ,
, ,
,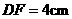 ,求:
,求:
(1)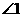 的度数;
的度数;
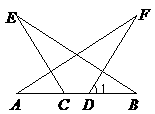 (2)
(2) 的长.
的长.
答案:(1)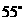 (2)
(2)
第26题. 如图所示, ,
,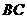 的延长线交
的延长线交 于
于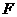 ,交
,交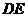 于
于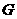 ,
,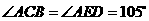 ,
,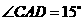 ,
,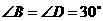 ,求
,求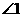 的度数.
的度数.

答案: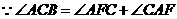
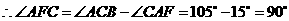
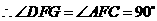
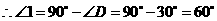 .
.
第27题. 已知: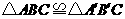 ,
, 的三边为
的三边为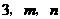 ,
,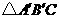 的三边为
的三边为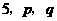 ,若
,若 的各边都是整数,则
的各边都是整数,则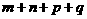 的最大值为多少?
的最大值为多少?
答案:由题意可知三边为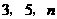 ,且
,且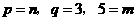 ,由于
,由于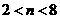 ,而
,而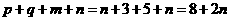 ,因此
,因此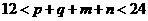 ,故最大整数值为
,故最大整数值为 .
.
第28题. 如图,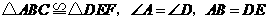 .找出另外两对相等的边和相等的角.
.找出另外两对相等的边和相等的角.

答案: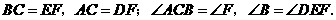
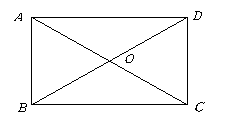
第29题. 矩形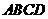 的对角线
的对角线 ,
, 相交于点
相交于点 ,指出图中所有的全等三角形.
,指出图中所有的全等三角形.
答案: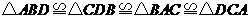 ;
;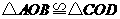 ,
,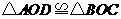 .
.
第30题. 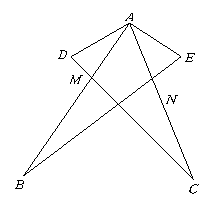
 与
与 全等,
全等,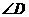 与
与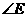 对应,顶点
对应,顶点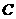 与
与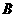 对应,写出其他对应角及对应顶点.
对应,写出其他对应角及对应顶点.
答案: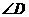 与
与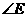 对应,顶点
对应,顶点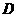 与
与 对应,顶点
对应,顶点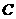 与
与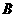 对应,所以
对应,所以 与
与 对应,则
对应,则 与
与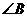 对应,
对应,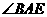 与
与 对应.
对应.
第31题. 小明在设计一份图纸时,需要把 以
以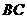 的中点
的中点 为中心,把
为中心,把 绕
绕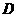 点旋转
点旋转 ,得到
,得到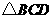 ,已知
,已知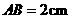 ,
,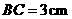 ,
,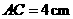 ,试求出
,试求出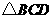 的三边长,并画图.
的三边长,并画图.
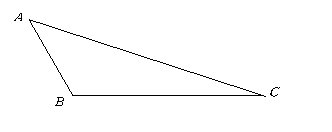
答案:因为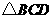 是通过
是通过 旋转得到的,所以
旋转得到的,所以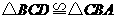 .
.
所以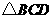 的三边长分别为
的三边长分别为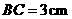 ,
,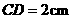 ,
,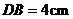 .
.
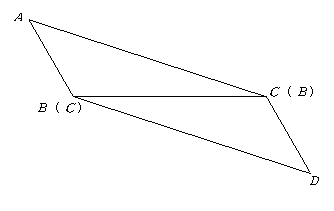 图形如下图.
图形如下图.
第32题. 如图, 中,
中,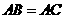 ,
,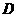 ,
, 在
在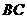 上,
上,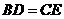 ,则图中全等三角形的对数是( )
,则图中全等三角形的对数是( )
 A.
A. B.
B.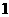 C.
C.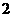 D.
D.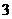
答案:C
第33题. 如图,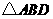 与
与 都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“
都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“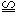 ”可以表示为( )
”可以表示为( )
A.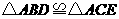 B.
B.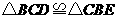
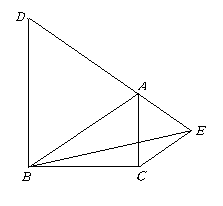 C.
C.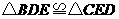 D.
D.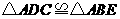
答案:D
第34题. 一个图案由一个正方形及其两条对角线组成,其中有 对全等三角形.
答案:8
第35题.  如图
如图 中,
中,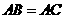 要使
要使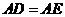 ,需要添加一个条件是 .
,需要添加一个条件是 .
答案: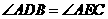 或
或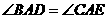 或
或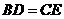 或
或 .
.
第36题. 如图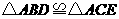 ,试说明
,试说明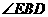 与
与 的关系.
的关系.

答案: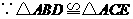 ,
,
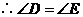 ,又
,又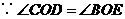 .
.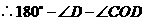
 .即
.即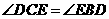 .
.
第37题. 已知 .
.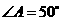 ,
,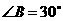 ,
,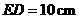 .试求
.试求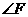 的度数及
的度数及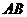 的长.
的长.
答案: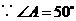 ,
,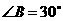 ,
,
 .
.
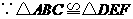 ,
,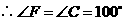 .
.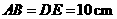 .
.
即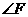 的度数是
的度数是 ,
,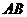 的长为
的长为 .
.
第38题. 如图, 与
与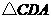 是全等三角形,则一定是一组对应边的是( )
是全等三角形,则一定是一组对应边的是( )
 A.
A.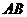 和
和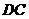 B.
B. 和
和 C.
C. 和
和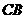 D.
D. 和
和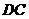
答案:B
第39题. 如图 为
为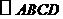 的对角线
的对角线 ,
, 的交点,
的交点,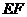 经过点
经过点 ,且与
,且与 ,
,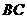 分别交于点
分别交于点 ,
,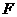 .若
.若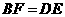 ,则图中全等三角形最多有( )
,则图中全等三角形最多有( )
A.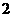 对 B.
对 B.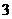 对 C.
对 C.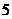 对 D.
对 D. 对
对
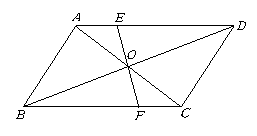
答案:D
第40题. 下列说法正确的是( )
A.若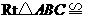
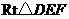 ,且
,且 的两条直角边分别是水平和竖直状态,那么
的两条直角边分别是水平和竖直状态,那么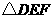 的两条直角边也一定分别是水平和竖直状态
的两条直角边也一定分别是水平和竖直状态
B.如果 ,
,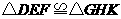 ,那么
,那么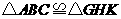
C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等
D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等
答案:B
第41题. 如果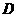 是
是 中
中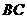 边上一点,并且
边上一点,并且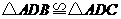 ,则
,则 是( )
是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
答案:D
第42题. 已知 ,
,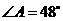 ,
,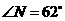 ,则
,则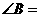 ,
, ,
,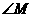 和
和 的度数分别为 , , .
的度数分别为 , , .
答案: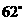 ;
;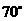 ,
,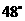 ,
,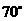
第43题. 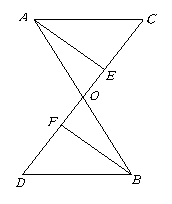 如图,在图中有3对全等三角形,分别是 , , .
如图,在图中有3对全等三角形,分别是 , , .
答案: ,
, ,
, .
.
第44题. 如图,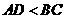 ,
,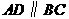 ,
,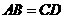 .
.
(1) 与
与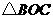 不可能全等,为什么?
不可能全等,为什么?
(2)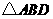 与
与 不可能全等,为什么?
不可能全等,为什么?

答案:(1) 与
与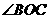 是对应角,它们所对的边不相等.
是对应角,它们所对的边不相等.
(2) 与
与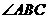 互补而不相等,
互补而不相等, 与
与 也不相等.
也不相等.
第45题. 如图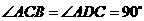 ,
, 与
与 不可能全等,请说明理由.
不可能全等,请说明理由.
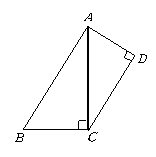
答案: 是两个三角形的公共边,它在
是两个三角形的公共边,它在 中是最大边,在
中是最大边,在 中不是最大边,所以
中不是最大边,所以 与
与 不可能全等.
不可能全等.
第46题. 如图所示,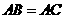 ,
,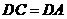 ,
,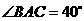 ,
,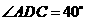 .
. 与
与 不可能全等,说明理由.
不可能全等,说明理由.

答案: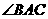 与
与 是对应角,夹它们的边不对应相等.
是对应角,夹它们的边不对应相等.
第47题. 如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
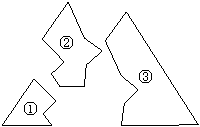
答案:C
6.(本题15分)如图16,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设 的度数为x,∠
的度数为x,∠ 的度数为
的度数为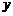 ,那么∠1,∠2
,那么∠1,∠2
的度数分别是多少?(用含有x或y的代数式表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.

5.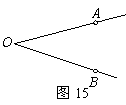 (本题13分)如图15,O为码头,A,B两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船从码头开出,计划沿∠AOB的平分线航行,航行途中,测得轮船与灯塔A,B的距离相等,此时轮船有没有偏离航线?画出图形并说明你的理由.
(本题13分)如图15,O为码头,A,B两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船从码头开出,计划沿∠AOB的平分线航行,航行途中,测得轮船与灯塔A,B的距离相等,此时轮船有没有偏离航线?画出图形并说明你的理由.
4.(本题12分)填空,完成下列证明过程.
如图14,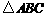 中,∠B=∠C,D,E,F分别在
中,∠B=∠C,D,E,F分别在 ,
,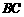 ,
, 上,且
上,且 ,
,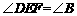
 求证:
求证: .
.
证明:∵∠DEC=∠B+∠BDE( ),
又∵∠DEF=∠B(已知),
∴∠______=∠______(等式性质).
在△EBD与△FCE中,
∠______=∠______(已证),
______=______(已知),
∠B=∠C(已知),
∴ ( ).
( ).
∴ED=EF( ).
3.(本题11分)如图13,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:
①分别在BA和CA上取 ;
;
②在BC上取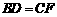 ;
;
③量出DE的长a米,FG的长b米.
如果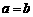 ,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?
,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?

2.(本题10分)已知:如图12,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,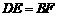 .
.
 求证:(1)
求证:(1) ;(2)
;(2) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com