
题目列表(包括答案和解析)
14.证明:延长BC至E,使CE=CD,∠DCE=60°,又CD=CE,则△CDE为等边三角形,故DE=CD=CE,∠CDE=60°,∵AB=AD,∠BAD=60°,∴△ABD为等边三角形
∴∠ADB=60°=∠CDE,∴∠ADC=∠BDE,又AD=BD∴△ADC≌△DBE,
∴AC=BE=BC+CE=BC+CD,即AC=BC+CD
(2)利用(1)的结论以AD为边向外作正△ADF边AC,可证明△CAF≌△BAD
13.延长CD至E,使DE=BD,连AE,∵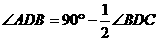 ,
,
∴∠BDC+2∠ADB=180°,∵∠BDC+∠BDA+∠ADE=180°,∴∠ADE=∠BDA,
又∵AD=AD,DE=DB,∴ △BDA≌△EDA,∴∠E=∠ABD=60°
AE=AB=AC,BD=CE,∴ △AEC为等边三角形,
∴ AE=AB=CE=CD+DE=CD+DB,即
AB=CD+DB
12.证:作DB的延长线至E,使AB=BE,连AE,则DE=DB+BA=CD,∵AD⊥CD,
∴△ACE为等腰三角形,∴∠C=∠E,∵△ABE为等腰三角形,∴∠ABD=∠E+∠BAE=2∠E,∠B=2∠C
7. b+c-a 8. -6 9. 4或5 10. 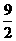 11. 108
11. 108
1.A 2. A 3. B 4. D 5. B 6. 45°
14.(1)如图(1), 四边形ABCD中,AB=AD,
∠BAD=60°,∠BCD=120°,证明:BC+DC=AC.
(2) 如图(2),四边形ABCD中,AB=BC,∠ABC=60°,P为四边形ABCD内一点,且∠APD=120°,证明:PA+PD+PC≥BD

|
|||
|
|||
13.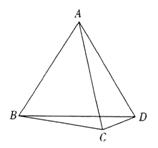 如图12,已知在△ABC中,AB=AC,
如图12,已知在△ABC中,AB=AC,
∠ABC>60°,∠ABD=60°,
|
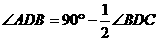 .求证:AB=BD+DC.
.求证:AB=BD+DC.
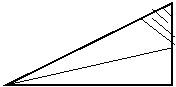
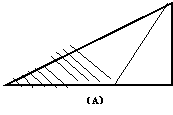
11.如图10,A,B是两个大小、形状相同的三角形纸片,其三边长之比为3:4:5,按如图方法将它们对折,使折痕过其中一个顶点,且使顶点所在两边重合,记折叠后不重合部分面积分别为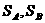 ,且
,且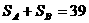 ,则三角形纸片A的面积为
.
,则三角形纸片A的面积为
.
 |
|||||
 |
|||||
|
 探索拓展
探索拓展
|
AB+BD=CD,求证:∠B=2∠C
9.一个等腰三角形的周长是12,且三长边长都是整数,则三角形的腰长是 .
|
 10.如图9,△ABC中,AB=AC=9,∠BAC=120°,
10.如图9,△ABC中,AB=AC=9,∠BAC=120°,
AD是△ABC的中线,AE是△ABD的角平分线,
DF∥AB交AE延长线于F,则DF的长为 .
8.如图8,在△ABC中,D是BC上的一点,
|
交AD于M,EF=12,则DM= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com