
题目列表(包括答案和解析)
4.一直角三角形的斜边比一直角边大2,另一直角边长为6,则斜边长为( )
A.8 B.10 C.12 D、13
3.函数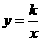 的图象经过点(一4,6),则下列各点中在该图象上的是( )
的图象经过点(一4,6),则下列各点中在该图象上的是( )
A.(3,8) B.(-8,-3) C、(3,-8) D、(-4,-6)
2.下列各式正确的是。( )
A.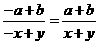 B、
B、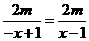
C.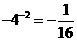 D、
D、
1.无论x取什么数,总是有意义的分式是( )
A、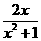 B、
B、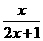 C、
C、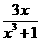 D、
D、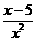
25、(1)∵A(3,m),B(n,6)在反比例函数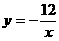 的图象上,
的图象上,
∴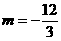 ,
,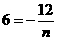 ,∴
,∴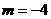 ,
,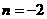 .
.
∴A(3,-4),B(-2,6). …………2分
(2)设直线AB的解析式为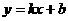 ,依题意,得
,依题意,得
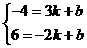 ,解得
,解得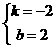 ,
,
∴直线AB的解析式为: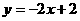 . …………5分
. …………5分
(3)当y=0时,-2x+2=0,得 x=1,∴C点坐标为(1,0).
∵ OA=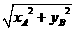 =
=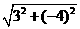 =5, …………6分
=5, …………6分
①当点D在x轴上时,设D(a,0),由CD=OA,得|a-1|=5,
解得a=6或a=-4; …………8分
②当点D在y轴上时,设D(0,b),由CD=OA,得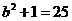
解得b=±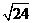 ;
;
∴ D的坐标为:(6,0),(-4,0),(0,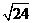 )或(0,-
)或(0,-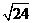 ).…………10分
).…………10分
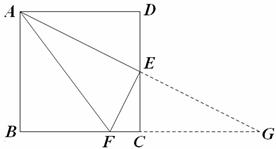
24、解:(1)证明:延长AE交BC的延长线于点G. …………1分
∵ 四边形ABCD是正方形,
∴ AD∥CG,∠D=∠BCD=∠DCG,
∴ ∠DAE=∠G
 ∵ ∠FAE=∠EAD,
∵ ∠FAE=∠EAD,
∴ ∠FAE=∠G
∴ AF=FG …………3分
∵ E是DC的中点
∴ DE=EC,
∵ ∠AED=∠GEC
∴ △AEF≌△GEF (ASA)
∴ AE=EG,
∴ EF⊥AE. …………5分
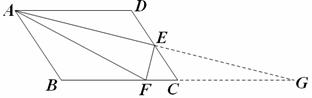
(2)若将(1)中的“正方形”改为“矩形”、“菱形”和“任意平行四边形”,其它条件不变,结论“EF⊥AE”仍然成立.例如:“任意平行四边形” …………6分
 …………8分
…………8分
如图,延长AE交BC的延长线于G,由AD∥BC,及E是DC的中点,可得△ADE≌GCE,得AE=EG,同(1)一样可得△AFG是等腰三角形,于是得FE⊥AG.…………9分
23、解:过D作DF∥AC,交BC的延长线于F,则四边形ACFD为平行四边形,
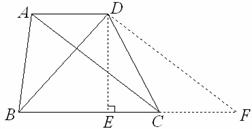 ∴ AC=DF=16,AD=CF=7; …………2分
∴ AC=DF=16,AD=CF=7; …………2分
在△DBF中,BD2+DF2=122+162=144+256=400,
BF2=400,∴BD2+DF2=BF2 ,
∴ △DBF是直角三角形,∠BDF=90° …………5分
过D作DE⊥BC于E,
∵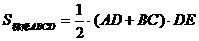 =
=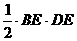 =
=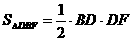 =96. …………9分
=96. …………9分
23.如图,在梯形ABCD中,AD∥BC,AD=7,BC=13,AC=16,BD=12,
求梯形ABCD的面积。
22、解:如图,设EF=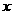
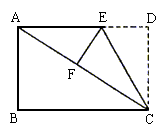 依题意知:△CDE≌△CFE, ………2分
依题意知:△CDE≌△CFE, ………2分
∴DE=EF=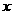 ,CF=CD=5,
,CF=CD=5,
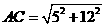 =13, …………4分
=13, …………4分
∴AF=AC-CF=8,AE=AD-DE=12-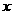 ,
,
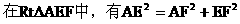
即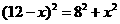 …………7分
…………7分
∴ 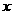 =
=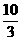 , 即EF=
, 即EF=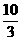 . …………8分
. …………8分
21、如图:
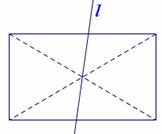
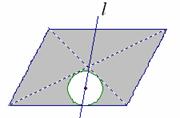 …………2分
…………2分
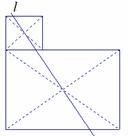
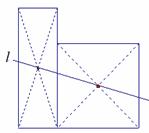
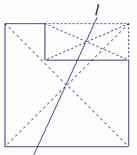 …………8分
…………8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com