4、　 直接写出因式分解的结果：

(1)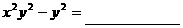；(2)。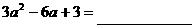

3、　 在括号前面填上“+”或“－”号，使等式成立：

(1)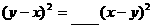；　　　 (2)。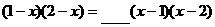

2、　 填上适当的式子，使以下等式成立：

(1)

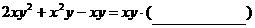
(2)

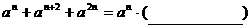
1、　 把下列各式的公因式写在横线上：

①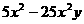、　　　　　　 ；　　　 ②=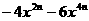　　 　

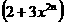
3．分解因式：

　(1)(2x²-3x+1)²-22x²+33x-1；

　(2)x⁴+7x³+14x²+7x+1；

　(3)(x+y)³+2xy(1-x-y)-1；

　(4)(x+3)(x²-1)(x+5)-20．

本资料由《七彩教育网》 提供！

3．分解因式：

　(1)(2x²-3x+1)²-22x²+33x-1；

　(2)x⁴+7x³+14x²+7x+1；

　(3)(x+y)³+2xy(1-x-y)-1；

　(4)(x+3)(x²-1)(x+5)-20．

第一讲 因式分解(一)

　多项式的因式分解是代数式恒等变形的基本形式之一，它被广泛地应用于初等数学之中，是我们解决许多数学问题的有力工具．因式分解方法灵活，技巧性强，学习这些方法与技巧，不仅是掌握因式分解内容所必需的，而且对于培养学生的解题技能，发展学生的思维能力，都有着十分独特的作用．初中数学教材中主要介绍了提取公因式法、运用公式法、分组分解法和十字相乘法．本讲及下一讲在中学数学教材基础上，对因式分解的方法、技巧和应用作进一步的介绍．

2．分解因式：

　(1)x³+3x²-4；

　(2)x⁴-11x²y²+y²；

　(3)x³+9x²+26x+24；

　(4)x⁴-12x+323．

1．分解因式：

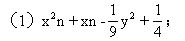
　(2)x¹⁰+x⁵-2；

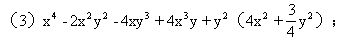
　(4)(x⁵+x⁴+x³+x²+x+1)²-x⁵．

3．换元法

　换元法指的是将一个较复杂的代数式中的某一部分看作一个整体，并用一个新的字母替代这个整体来运算，从而使运算过程简明清晰．

　例6 分解因式：(x²+x+1)(x²+x+2)-12．

　分析 将原式展开，是关于x的四次多项式，分解因式较困难．我们不妨将x²+x看作一个整体，并用字母y来替代，于是原题转化为关于y的二次三项式的因式分解问题了．

　解 设x²+x=y，则

　原式=(y+1)(y+2)-12=y²+3y-10

　　=(y-2)(y+5)=(x²+x-2)(x²+x+5)

　　=(x-1)(x+2)(x²+x+5)．

　说明 本题也可将x²+x+1看作一个整体，比如今x²+x+1=u，一样可以得到同样的结果，有兴趣的同学不妨试一试．

　例7 分解因式：

(x²+3x+2)(4x²+8x+3)-90．

　分析 先将两个括号内的多项式分解因式，然后再重新组合．

　解 原式=(x+1)(x+2)(2x+1)(2x+3)-90

　　　 =[(x+1)(2x+3)][(x+2)(2x+1)]-90

　　　 =(2x²+5x+3)(2x²+5x+2)-90．

　令y=2x²+5x+2，则

　原式=y(y+1)-90=y²+y-90

　　=(y+10)(y-9)

　　=(2x²+5x+12)(2x²+5x-7)

　　=(2x²+5x+12)(2x+7)(x-1)．

　说明 对多项式适当的恒等变形是我们找到新元(y)的基础．

　例8 分解因式：

(x²+4x+8)2+3x(x²+4x+8)+2x²．

　解 设x²+4x+8=y，则

　原式=y²+3xy+2x²=(y+2x)(y+x)

　　=(x²+6x+8)(x²+5x+8)

　　=(x+2)(x+4)(x²+5x+8)．

　说明 由本题可知，用换元法分解因式时，不必将原式中的元都用新元代换，根据题目需要，引入必要的新元，原式中的变元和新变元可以一起变形，换元法的本质是简化多项式．

　例9 分解因式：6x⁴+7x³-36x²-7x+6．

　解法1 原式=6(x⁴+1)+7x(x²-1)-36x²

　　　　=6［(x⁴-2x²+1)+2x²］+7x(x²-1)-36x²

　　　　=6[(x²-1)2+2x²]+7x(x²-1)-36x²

　　　　=6(x²-1)²+7x(x²-1)-24x²

　　　　=[2(x²-1)-3x］［3(x²-1)+8x]

　　　　=(2x²-3x-2)(3x²+8x-3)

　　　　=(2x+1)(x-2)(3x-1)(x+3)．

　说明 本解法实际上是将x²-1看作一个整体，但并没有设立新元来代替它，即熟练使用换元法后，并非每题都要设置新元来代替整体．

　解法2

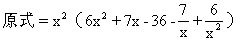
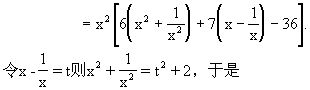
　原式=x²[6(t²+2)+7t-36]

　　=x²(6t²+7t-24)=x²(2t-3)(3t+8)

　　=x²[2(x-1/x)-3][3(x-1/x)+8]

　　=(2x²-3x-2)(3x²+8x-3)

　　=(2x+1)(x-2)(3x-1)(x+3)．

　例10 分解因式：(x²+xy+y²)-4xy(x²+y²)．

　分析 本题含有两个字母，且当互换这两个字母的位置时，多项式保持不变，这样的多项式叫作二元对称式．对于较难分解的二元对称式，经常令u=x+y，v=xy，用换元法分解因式．

　解 原式=[(x+y)²-xy]²-4xy[(x+y)²-2xy]．令x+y=u，xy=v，则

　原式=(u²-v)²-4v(u²-2v)

　　=u⁴-6u²v+9v²

　　=(u²-3v)²

　　=(x²+2xy+y²-3xy)²

　　=(x²-xy+y²)²．

练习一

2．拆项、添项法

　因式分解是多项式乘法的逆运算．在多项式乘法运算时，整理、化简常将几个同类项合并为一项，或将两个仅符号相反的同类项相互抵消为零．在对某些多项式分解因式时，需要恢复那些被合并或相互抵消的项，即把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符合相反的项，前者称为拆项，后者称为添项．拆项、添项的目的是使多项式能用分组分解法进行因式分解．

　例4 分解因式：x³-9x+8．

　分析 本题解法很多，这里只介绍运用拆项、添项法分解的几种解法，注意一下拆项、添项的目的与技巧．

　解法1 将常数项8拆成-1+9．

　原式=x³-9x-1+9

　　=(x³-1)-9x+9

　　=(x-1)(x²+x+1)-9(x-1)

　　=(x-1)(x²+x-8)．

　解法2 将一次项-9x拆成-x-8x．

　原式=x³-x-8x+8

　　=(x³-x)+(-8x+8)

　　=x(x+1)(x-1)-8(x-1)

　　=(x-1)(x²+x-8)．

　解法3 将三次项x³拆成9x³-8x³．

　原式=9x³-8x³-9x+8

　　=(9x³-9x)+(-8x³+8)

　　=9x(x+1)(x-1)-8(x-1)(x²+x+1)

　　=(x-1)(x²+x-8)．

　解法4 添加两项-x²+x²．

　原式=x³-9x+8

　　=x³-x²+x²-9x+8

　　=x²(x-1)+(x-8)(x-1)

　　=(x-1)(x²+x-8)．

　说明 由此题可以看出，用拆项、添项的方法分解因式时，要拆哪些项，添什么项并无一定之规，主要的是要依靠对题目特点的观察，灵活变换，因此拆项、添项法是因式分解诸方法中技巧性最强的一种．

　例5 分解因式：

　(1)x⁹+x⁶+x³-3；

　(2)(m²-1)(n²-1)+4mn；

　(3)(x+1)⁴+(x²-1)²+(x-1)⁴；

　(4)a³b-ab³+a²+b²+1．

　解 (1)将-3拆成-1-1-1．

　原式=x⁹+x⁶+x³-1-1-1

　　=(x⁹-1)+(x⁶-1)+(x³-1)

　　=(x³-1)(x⁶+x³+1)+(x³-1)(x³+1)+(x³-1)

　　=(x³-1)(x6+2x3+3)

　　=(x-1)(x²+x+1)(x⁶+2x³+3)．

　(2)将4mn拆成2mn+2mn．

　原式=(m²-1)(n²-1)+2mn+2mn

　　=m²n²-m²-n²+1+2mn+2mn

　　=(m²n²+2mn+1)-(m²-2mn+n²)

　　=(mn+1)²-(m-n)²

　　=(mn+m-n+1)(mn-m+n+1)．

　(3)将(x²-1)²拆成2(x²-1)²-(x²-1)²．

　原式=(x+1)⁴+2(x²-1)²-(x²-1)²+(x-1)⁴

　　=［(x+1)⁴+2(x+1)²(x-1)²+(x-1)⁴]-(x²-1)²

　　=［(x+1)²+(x-1)²]²-(x²-1)²

　　=(2x²+2)²-(x²-1)²=(3x²+1)(x²+3)．

　(4)添加两项+ab-ab．

　原式=a³b-ab³+a²+b²+1+ab-ab

　　=(a³b-ab³)+(a²-ab)+(ab+b²+1)

　　=ab(a+b)(a-b)+a(a-b)+(ab+b²+1)

　　=a(a-b)［b(a+b)+1]+(ab+b²+1)

　　=[a(a-b)+1](ab+b²+1)

　　=(a²-ab+1)(b²+ab+1)．

　说明 (4)是一道较难的题目，由于分解后的因式结构较复杂，所以不易想到添加+ab-ab，而且添加项后分成的三项组又无公因式，而是先将前两组分解，再与第三组结合，找到公因式．这道题目使我们体会到拆项、添项法的极强技巧所在，同学们需多做练习，积累经验．