⒋若函数y=(m－1)x^|m|－2－1是关于x的一次函数，且y随x的增大而减小，则m=________.

⒌若一次函数的图象经过点(1，3)与(2，－1)，则它的解析式为___________________，函数y随x的增大而____________.

⒍一次函数y=2x－3的图象可以看作是函数y=2x的图象向__________平移________个单位长度得到的，它的图象经过_______________象限，y随x的增大而___________.

⒎ 已知一次函数y=kx－1的图象不经过第二象限，则正比例函数y=(k+1)x必定经过　　　 第______________象限.

三、　　　　　　 解答题 ⒏ 已知一次函数y=(2m+4)x+(3－n). ⑴当m、n是什么数时，y随x的增大而增大？ ⑵当m、n是什么数时，函数图象经过原点？ ⑶若图象经过一、二、三象限，求m、n的取值范围. 　 　 　 　 　 　 ⒐已知一次函数y=(3m－7)x+m－1的图象与y轴交点在x轴的上方，且y随x的增大而减小，求整数m的值. 　 　 　 　 　 　 　 　 ⒑作出函数y=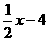的图象，并根据图象回答问题： ⑴当x取何值时，y>0? ⑵当－1≤x≤2时，求y的取值范围.

4.某公司计划在”五一”期间组织员工到某地旅游,参加旅游的人数估计为10-25人,甲,乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠,乙旅行社表示可免去一位游客的旅游费用,其余游客八五折优惠,该公司选择哪家旅行社支出的费用较少?(提示:设参加旅游人数为人时,甲,乙两家旅行社的费用为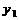,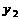元)

3.某移动公司为用户提供两种资费方式拨打市话.甲:拨打和接听市话0.40元/min,但每月要交50元月租费;乙:拨打和接听市话0.60元/min,不收月租费.

(1)分别写出两种资费方式下的费用 (元)与拨打或接听电话时间 (min) 之间的关系式;

(2)在同一直角坐标系中画出它们的图象;

(3)若某人每月需使用手机通话200min,选择哪种付费方式能合算一些?若某人计划每月花费160元手机话费,选择哪种付费方式能多使用一些时间?

2.某图书馆开展两种方式的租书业务:一是使用会卡,另一种是不使用会员卡.采用这两种方式,租书金额与租书时间之间的关系如图所示:

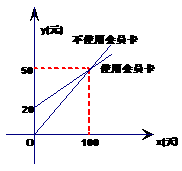(1)分别写出不使用会员卡和使用会员卡租书的金额 (元)与租书时间 (天)之间的函数关系式;

(2)两种租书方式每天租书的费用分别是多少?当租书时间为多少　　 天时两种租书费用相等?

(3)若会员卡的使用期限是一年,而需借书150天,则采用哪种方式比较划算?

1.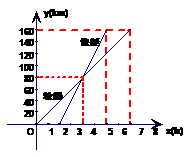 如图表示一艘轮船和一艘快艇沿相同的路线从甲港出发到乙港行驶路程和时间变化的图象，根据图象回答下列问题：

(1)快艇比轮船晚出发几小时？比轮船早几小时

到达乙港？

(2)轮船和快艇在途中的(不包括起点和终点)的

行驶速度分别是多少？

(3)快艇出发多长时间赶上轮船？

6.某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用 (元)是行李质量 (㎏)的一次函数,其图象如图所示,

(1)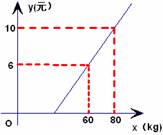求与之间的函数关系式;

(2)旅客最多可免费携带多少千克的行李?

§5.4一次函数的应用(2)

5.某礼堂有若干排座位,已知每排的座位数是这排的排数的一次函数,第1排有20个座位,第19排有56个座位,

(1)写出与之间的函数关系式;

(2)第26排有多少个座位?

4.在弹性限度内,弹簧长度 (㎝)是所挂物体质量 (㎏)的一次函数,不挂物体时,弹簧长是14.5㎝,所挂物体质量每增加1㎏弹簧长度增加0.5㎝,现弹簧上挂一物体,弹簧长度为17.5㎝,试求所挂物体的质量.

3.某空调公司推销员的月收入与每月的销售量成一次函数关系.当他售出10件商品时收入为800元,当售出20件时收入为1300元,试问此销售员没有销售时可收入多少元?

2.为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的,研究表明;假设椅子的高度(不含靠背)为(㎝),课桌的高度为 (㎝),则应是的一次函数,下表列出两套符合条件的课桌椅的高度:

(1)试确定与之间的函数关系式;

(2)现有一把高42.0㎝的椅子和一张高78.2㎝的课桌,它们是否配套?请通过计算说明理由.