
题目列表(包括答案和解析)
20、(本小题满分12分)
已知圆C: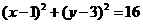 ,直线
,直线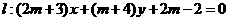
(1) 无论m取任何实数,直线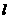 必经过一个定点,求出这个定点的坐标。
必经过一个定点,求出这个定点的坐标。
(2) 当m取任意实数时,直线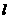 和圆的位置关系有无不变性,试说明理由。
和圆的位置关系有无不变性,试说明理由。
(3) 请判断直线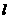 被圆C截得的弦何时最短,并求截得的弦最短时m的值以及弦的长度
被圆C截得的弦何时最短,并求截得的弦最短时m的值以及弦的长度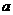 .
.
解:(1) 直线: 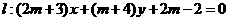
可变形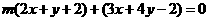
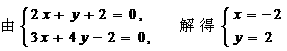 。 因此直线
。 因此直线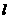 恒过定点P(-2,2)
恒过定点P(-2,2)
(2) 因为已知圆的圆心C(1,3),半径r=4, 而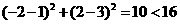 ,
,
所以直线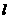 过圆C
过圆C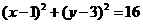 内一定点
内一定点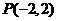 ,
,
故不论m取何值,直线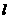 和圆总相交
和圆总相交
(3)当直线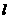 垂直于CP时,截得的弦最短,此时,
垂直于CP时,截得的弦最短,此时,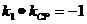
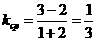 ,
, 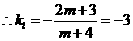 ,得
,得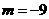 .
.
 ∴ 最短弦长为
∴ 最短弦长为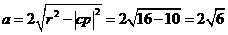 所以
所以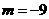 ,
, 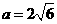
19、(本小题满分12分)
已知函数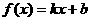 的图象与
的图象与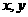 轴分别相交于点A、B,
轴分别相交于点A、B,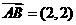 ,函数
,函数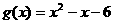 。
。
(1)求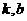 的值; (2)当
的值; (2)当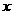 满足
满足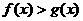 时,求函数
时,求函数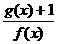 的最小值。
的最小值。
解:(1)由已知得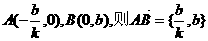
于是
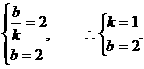
(2)由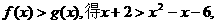
即
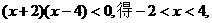
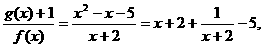
由于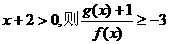 ,其中等号当且仅当x+2=1,即x=-1时成立,
,其中等号当且仅当x+2=1,即x=-1时成立,
∴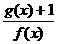 时的最小值是-3.
时的最小值是-3.
18、(本小题满分12分)
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD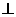 平面PEG
平面PEG
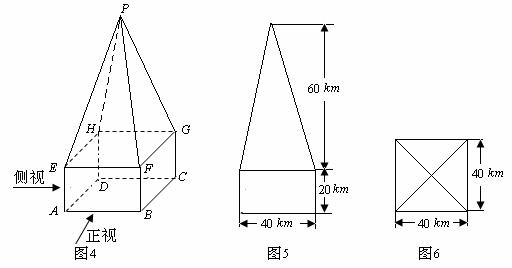
[解析](1)侧视图同正视图,如下图所示.
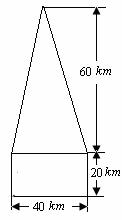
(2)该安全标识墩的体积为: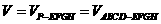
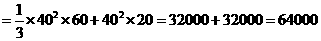
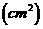
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, 平面EFGH ,
平面EFGH , 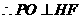
又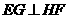
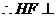 平面PEG
平面PEG
又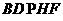
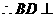 平面PEG;
平面PEG;
17、(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且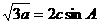
(Ⅰ)确定角C的大小:
(Ⅱ)若c=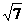 ,且△ABC的面积为
,且△ABC的面积为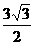
 ,求a+b的值。
,求a+b的值。 


16、设函数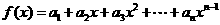 ,
,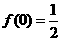 ,数列
,数列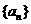 满足
满足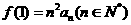 ,则数列
,则数列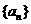 的通项
的通项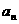 等于
等于
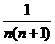
15、直线l与圆x2+y2+2x-4y+a=0(a<3)相交于两点A,B,弦AB的中点为(0,1),则直线l的方程为 x-y+1=0 .
14、空间四边形ABCD中,AC与BD成600角,AC=8,BD=8,M,N分别为AB,CD的中点,则线段MN的长是 4或4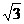 。
。 

13、某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号, ,196~200号)。若第5组抽出的号码为22,则第8组抽出的号码应是
。若用分层抽样方法,则40岁以下年龄段应抽取
人。
,196~200号)。若第5组抽出的号码为22,则第8组抽出的号码应是
。若用分层抽样方法,则40岁以下年龄段应抽取
人。
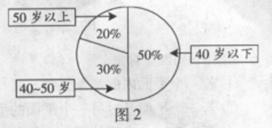


[答案]37, 20
[解析]由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为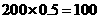 ,则应抽取的人数为
,则应抽取的人数为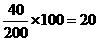 人.
人.
12、若实数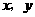 满足
满足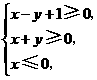 则
则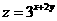 的最小值是( B )
的最小值是( B ) 

A、0 B、1 C、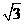 D、9
D、9
11、设a,b,c分别是△ABC中,∠A,∠B,∠C所对边的边长,则直线sinA·x+ay+c=0与bx-sinB·y+sinC=0的位置关系是( C )
A、平行 B、重合 C、垂直 D、相交但不垂直
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com