
题目列表(包括答案和解析)
20.(本小题满分12分)
解:(Ⅰ)设圆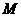 的方程为:
的方程为: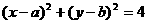 ........1分
........1分
根据题意得: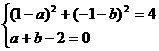 ........3分
........3分
解得;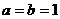 或
或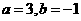
因为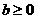 ,所以
,所以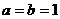
故所求圆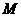 的方程为:
的方程为: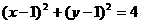 ........6分
........6分
(Ⅱ)设直线与圆交于 、
、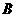 两点
两点
联立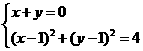 解得
解得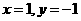 或
或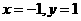
所以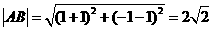 ........8分
........8分
因为三角形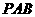 面积
面积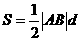
要使三角形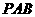 面积最大,只要求出其最大距离
面积最大,只要求出其最大距离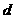 即可.
即可.
根据平面几何的性质可知,距离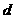 为最大时,
为最大时,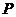 点为弦
点为弦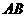 的垂直平分线与圆的交点
的垂直平分线与圆的交点
此时最大距离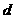 等于圆心
等于圆心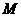 到直线
到直线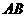 的距离
的距离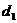 加上圆的半径......10分
加上圆的半径......10分
则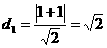
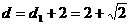 ,所以
,所以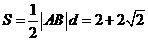
所以三角形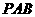 面积的最大值为
面积的最大值为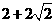 .......12分
.......12分
19. (本小题满分12分)
(本小题满分12分)
解:设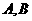 两种不同的货物分别装载
两种不同的货物分别装载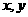 吨,则
吨,则

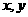 满足的关系式为
满足的关系式为 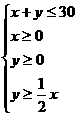 ①
①
所以①所示的线性区域如右图........5分
由已知目标函数为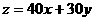 即
即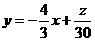 .......7分
.......7分
 当直线
当直线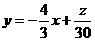 在线性区域内在
在线性区域内在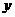 轴的截距最大时,
轴的截距最大时, 最大......9分
最大......9分
解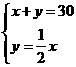 得
得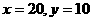
如图可知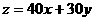 在
在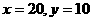 最大
最大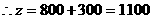
 当装载
当装载 、
、 货物分别为
货物分别为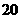 吨、
吨、 吨时,载货收入最大,最大值为
吨时,载货收入最大,最大值为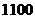 元...12分
元...12分
18. (本小题满分12分)
解:(Ⅰ) 向量
向量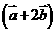 与向量
与向量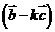 垂直
垂直

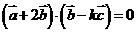 .....2分
.....2分
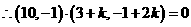
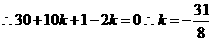 .....5分
.....5分
(Ⅱ)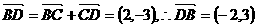 .......7分
.......7分
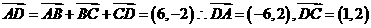 .......9分
.......9分

 ,
,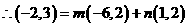
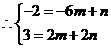
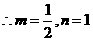 .......12分
.......12分
17.(本小题满分12分)
解:(Ⅰ)
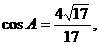
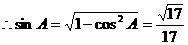
则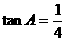 .....2分
.....2分
所以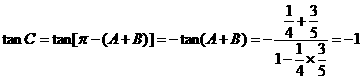 .....5分
.....5分
(Ⅱ)因为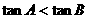 ,且
,且 、
、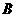 均为锐角
均为锐角
又由(Ⅰ)知: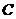 为钝角,所以
为钝角,所以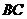 为最小边,
为最小边,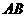 为最大边.....6分
为最大边.....6分
由(Ⅰ)可求得: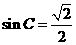
由正弦定理得: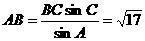
所以最大边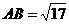 .....8分
.....8分
因为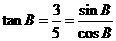 ,
,
所以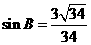 .....10分
.....10分
所以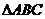 的面积为
的面积为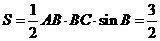 .....12分
.....12分
13.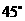 ; 14.
; 14.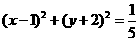 ; 15.
; 15.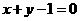 ;
16.
;
16.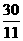
D B A D B D A D CC C B
22.(本题满分14分)
在数列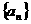 中,首项
中,首项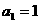 ,前
,前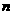 项和
项和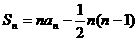 ,
,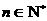 .
.
(Ⅰ)求证:数列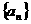 为等差数列;
为等差数列;
(Ⅱ)若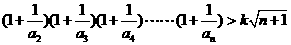 对一切
对一切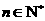 且
且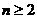 恒成立,求实数
恒成立,求实数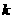 的取值范围.
的取值范围.
2009年教学质量检测
高一数学答案及评分标准
21.(本题满分12分)
解关于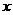 的不等式:
的不等式: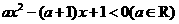 .
.
20.(本题满分12分)
已知直径为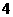 的圆
的圆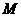 过点
过点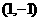 ,且圆心
,且圆心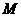 在射线:
在射线: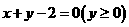 上.
上.
(Ⅰ)求圆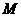 的方程;
的方程;
(Ⅱ)设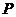 是圆
是圆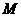 上的动点,直线
上的动点,直线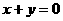 与圆
与圆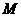 交于不同的两点
交于不同的两点 、
、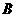 ,求三角形
,求三角形
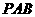 面积的最大值.
面积的最大值.
19.(本题满分12分)
一辆货车的最大载重量为 吨,要装载
吨,要装载 、
、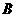 两种不同的货物,已知装载
两种不同的货物,已知装载 货物每吨收入
货物每吨收入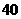 元,装载
元,装载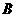 货物每吨收入
货物每吨收入 元,且要求装载的
元,且要求装载的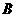 货物不少于
货物不少于 货物的一半.请问
货物的一半.请问 、
、 两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com