
02.下列图案中不是轴对称图形的是[ ]
A. B.
B. C.
C. D.
D.
一、选择题
01.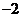 的倒数是[ ]
的倒数是[ ]
A.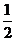 B.
B.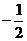 C.
C.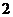 D.
D.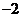
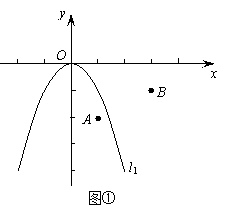
2.如图①,在平面 直角坐标系中,点
直角坐标系中,点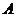 的坐标为(
的坐标为(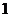 ,
,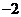 ),点
),点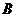 (3,
(3,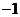 ),二次函数
),二次函数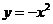 的图象为
的图象为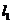 。
。
(1)平移抛物线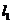 ,使平
,使平 移后的抛物线经过点
移后的抛物线经过点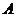 ,但不经过点
,但不经过点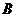 。
。
①满足此条件的函数解析式有 个;
②写出向下平移且过点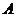 的解析式
。
的解析式
。
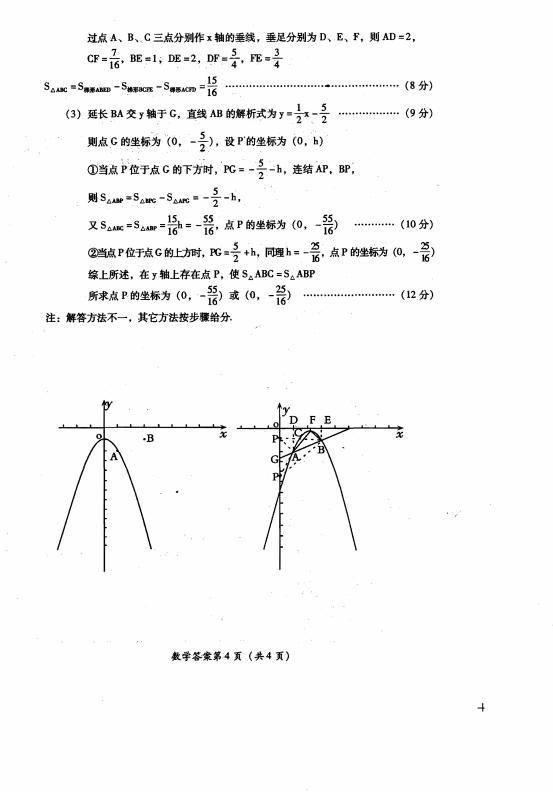
(2)平移抛物线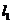 ,使平移后的抛物线经过
,使平移后的抛物线经过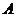 、
、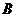 两点,所得的抛物线为
两点,所得的抛物线为 ,如图②,求抛物线
,如图②,求抛物线 的解析式及顶点坐标,并求
的解析式及顶点坐标,并求 的面积;
的面积;
(3)在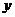 轴上是否存在点
轴上是否存在点 ,使
,使 ,若存在,求出点
,若存在,求出点 的坐标;若不存在,请说明好理由。
的坐标;若不存在,请说明好理由。






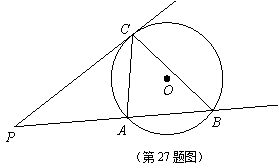
1.已知:如图, 是
是 外一点,过点
外一点,过点 引圆的切线
引圆的切线 (
(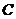 为切点)和割线
为切点)和割线 ,分别交
,分别交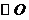 于
于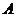 、
、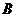 ,连接
,连接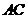 、
、 。
。
(1)求证: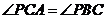 ;
;
(2)利用 (1)的结论,已知
(1)的结论,已知 ,
,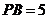 ,求
,求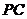 的长。
的长。
2.如图,圆柱形容器高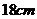 ,底面周长为
,底面周长为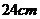 ,在杯内壁离杯底
,在杯内壁离杯底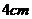 的点
的点 处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿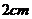 与与密封相对的
与与密封相对的 处,则蚂蚁从外壁
处,则蚂蚁从外壁 处到达内壁
处到达内壁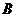 处的最短距离为
处的最短距离为
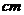 。
。
 七、解答题:(共2
七、解答题:(共2 小题,27题8分,28题12分,共20分)
小题,27题8分,28题12分,共20分)
1. 关于
关于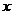 的方程
的方程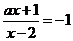 的解是正数,则
的解是正数,则 的取值范围是
。
的取值范围是
。
2.我州某校计划购买甲、乙两种树苗共1000株用以绿化校园。甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲、乙两种树苗的成活率分别是90%和95%。
(1)若购买这两种树苗共用去28000元,则甲、乙两种树苗各购买多少株?
(2)要使这批树苗的成活率不低于92%,则甲种树苗最多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用。
B卷(共30分)
 六、填空题:(共2小题,每小题5分,共10分)
六、填空题:(共2小题,每小题5分,共10分)
1.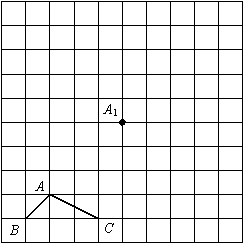 如图所示,正方形网格中,
如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上)。
为格点三角形(即三角形的顶点都在格点上)。
(1)把 沿
沿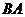 方向平移后,点
方向平移后,点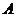 移到点
移到点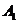 ,在网格中画出平移后得到的
,在网格中画出平移后得到的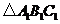 ;
;
(2)把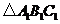 绕点
绕点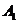 按逆时针旋转
按逆时针旋转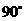 ,在网格中画出旋转后的
,在网格中画出旋转后的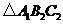 ;
;
(3)如果网格中小正方形的白南昌为1,求点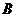 经过(1)、(2)变换的路径总长。
经过(1)、(2)变换的路径总长。
3. 实验与探究:
三角点阵中前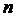 行的点数计算
行的点数计算
 下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……,第
下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……,第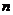 行有
行有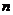 个点……
个点……
……
容易发现,10 是三角点阵中前4行的点数之和。你能发现300是前多少行的点数之和吗?
是三角点阵中前4行的点数之和。你能发现300是前多少行的点数之和吗?
如果用实验的方法,由上而下地逐行相加其点数,虽然你能发现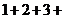 …
…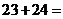 300,得知300是前24行的点数之和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
300,得知300是前24行的点数之和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
我们先探究三角点阵中前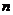 行的点数和与
行的点数和与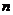 的数量关系。
的数量关系。
前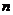 行的点数和
行的点数和 是
是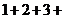 …
… ,可以发现,
,可以发现,
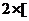
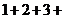 …
…
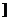
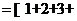 …
…
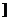 +
+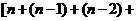 …
…
把两个中括号中的第一项相加,第二项相加……第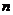 项相加,上式等号的后边变形为这
项相加,上式等号的后边变形为这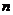 个小括号都等于
个小括号都等于 ,整个式子等于
,整个式子等于 ,于是得到
,于是得到
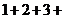 …
…

这就是说,三角点阵中前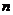 行的点数的和是
行的点数的和是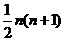 。
。
下面用一元二次方程解决上述问题:
设三角点阵中前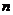 行的点数和为300,则有
行的点数和为300,则有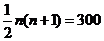 ,
,
整理这个方程,得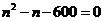 ,
,
解方程得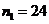 ,
,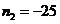 。
。
根据问题中未知数的意义确定 ,即三角点阵中前
,即三角点阵中前 项的和是300.
项的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前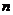 行的点数和能是600吗?如果能,求出
行的点数和能是600吗?如果能,求出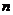 ;如果不能,试用一元二次方程说明道理;
;如果不能,试用一元二次方程说明道理;
(2)如果把图中的三角点阵中各行的点数依次换为2、4、6、……、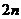 ,你能探究出前
,你能探究出前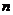 行的点数之和满足什么规律吗?这个三角点阵中前
行的点数之和满足什么规律吗?这个三角点阵中前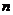 行的点数之和能是600吗?如果能,求出
行的点数之和能是600吗?如果能,求出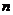 ;如果不能,试用一元二次方程说明道理。
;如果不能,试用一元二次方程说明道理。
 五、解答题:(共2小题,每小题8分,共16分)
五、解答题:(共2小题,每小题8分,共16分)
2. 如图,分别以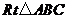 的直角边
的直角边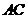 及斜边
及斜边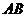 向外作等边
向外作等边 及等边
及等边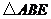 ,已知:
,已知: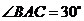 ,
,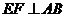 ,垂足为
,垂足为 ,连接
,连接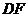 。
。
(1)是说明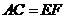 ; (2)求证:四边形
; (2)求证:四边形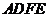 是平行四边形。
是平行四边形。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com