
25.(本小题满分l0分)
将两块含30°角且大小相同的直角三角板如图l摆放。
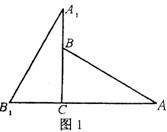
(1)将图l中△A1B1C绕点C顺时针转45°得到图2,点Pl是A1C与AB的交点,求证: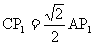
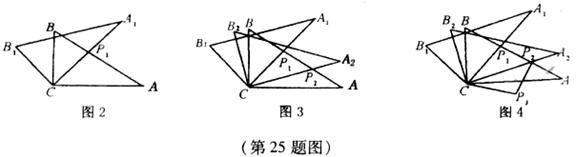
(2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3),P2是A2C与AB的交点,线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个等量关系式,并说明理由;
(3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4)连结P3P2,求证:P3P2⊥AB。
24.(本小题满分l0分)
元旦晚会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
纸环数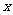 (个) (个) |
1 |
2 |
3 |
4 |
… |
彩纸链长度 (cm) (cm) |
19 |
36 |
53 |
70 |
… |
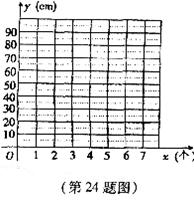
(1)把上表中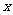 ,
, 的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想 与
与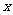 的函数关系,并求出函数表达式。
的函数关系,并求出函数表达式。
(2)教室天花板对角线长l0m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
23.(本小题满分8分)
 小杰到学校食堂买饭,看到A,B两窗口前面排队的人数一样多(设为
小杰到学校食堂买饭,看到A,B两窗口前面排队的人数一样多(设为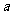 人,
人,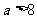 ),就站到A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
),就站到A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含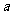 的代数式表示)
的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口队伍后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求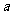 的取值范围。(不考虑其他因素)
的取值范围。(不考虑其他因素)
22.(本小题满分6分)
2007年春季房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷,共发放1200份调查问卷,实际收回l000份,该房地产公司根据问卷情况,作了以下两方面统计:
I.根据被调查消费者年收入情况制成统计表:
|
年收入(元) |
2万以下 |
2万~4万 (不含4万) |
4万~6万 (不含6万) |
6万~8万 (不含8万) |
8万以上 |
|
各段被调查消费者人数占总被调查消费者人数的百分比 |
50% |
26% |
14% |
7% |
3% |
Ⅱ.根据被调查消费者打算购买不同住房面积的人数情况制成的扇形统计图:

根据上述信息,解决下列问题:
(1)被调查的消费者平均年收入为多少万元?(提示:在计算时,2万元以下的都看成1万元,2万~4万元的都看成3万元,依此类推,8万以上的都看成9万元)
(2)打算购买80~l00m2的消费者人数为多少人?
(3)如果你是该房地产公司的开发商,请你从建房面积等方面谈谈今后的工作打算。(不超过30字)
21.(本小题满分7分)
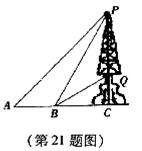
如图,从地面上的一点A测得山顶电视发射塔的上端P点的仰角是45°,向前走60m到达B点,测得P点的仰角是60°,电视塔底部Q点的仰角是30°,求电视发射塔PQ的高度。(结果保留根号)
20.(本小题满分7分)
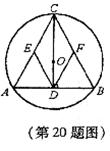
已知:如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点。求证:四边形CEDF是菱形。
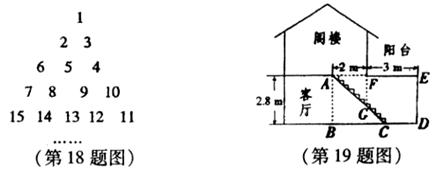
19.汪老师要装修自己带阁楼的新居(图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯竖直距离FG为1.75m。他量得客厅AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m,则楼梯底端C到墙角D的距离CD是 m。
18.一系列数如图排列,第四行最大的数是l0,第五行最大的数是15,照此排列规律,第六行最大的数是 ,第n行最大的数是 (用含n的代数式表示)。
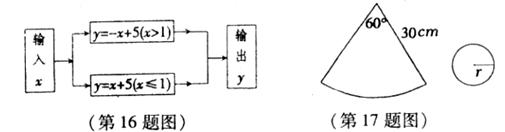
17.如图,有一个扇形和一个圆形纸片,扇形的圆心角为60°,半径为30cm若用这两张纸片围成一个圆锥,则圆形纸片的半径应为 cm。
16.根据如图的程序,计算当输入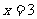 时,输出的结果
时,输出的结果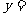 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com