
2.下列各式中计算结果等于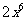 的是( )
的是( )
A. B.
B.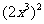 C.
C.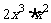 D.
D.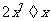
1.4的平方根是( )
A.2 B.4 C. D.
D.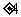
25.(12分)
如图,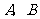 分别为
分别为 轴和
轴和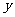 轴正半轴上的点,
轴正半轴上的点,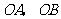 的长分别是方程
的长分别是方程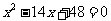 的两根(
的两根(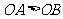 ),直线
),直线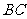 平分
平分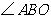 交
交 轴于
轴于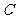 点,
点, 为
为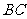 上一动点,
上一动点, 点以每秒
点以每秒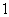 个单位的速度从
个单位的速度从 点开始沿
点开始沿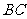 方向移动.
方向移动.
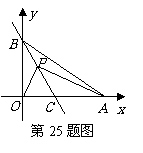 (1)设
(1)设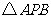 和
和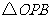 的面积分别为
的面积分别为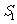 ,
,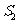 ,求
,求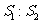 的值;
的值;
(2)求直线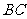 的解析式;
的解析式;
(3)设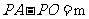 ,
, 点的移动时间为
点的移动时间为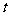 .
.
①当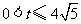 时,试求出
时,试求出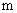 的取值范围;
的取值范围;
②当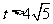 时,你认为
时,你认为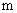 的取值范围如何(只要求写出结论)?
的取值范围如何(只要求写出结论)?
24.(10分)
(1)已知矩形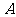 的长、宽分别是2和1,那么是否存在另一个矩形
的长、宽分别是2和1,那么是否存在另一个矩形 ,它的周长和面积分别是矩形
,它的周长和面积分别是矩形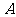 的周长和面积的2倍?
的周长和面积的2倍?
 对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决,小明论证的过程开始是这样的:如果用
对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决,小明论证的过程开始是这样的:如果用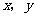 分别表示矩形的长和宽,那么矩形
分别表示矩形的长和宽,那么矩形 满足
满足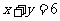 ,
,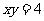 .
.
请你按照小明的论证思路完成后面的论证过程.
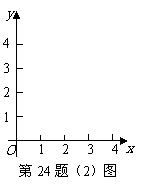 (2)已知矩形
(2)已知矩形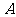 的长和宽分别是2和1,那么是否存在一个矩形
的长和宽分别是2和1,那么是否存在一个矩形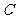 ,它的周长和面积分别是矩形
,它的周长和面积分别是矩形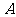 的周长和面积的一半?
的周长和面积的一半?
小明认为这个问题是肯定的,你同意小明的观点吗?为什么?
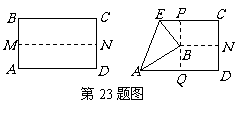
23.(10分)
如图,先把一矩形 纸片对折,设折痕为
纸片对折,设折痕为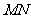 ,再把
,再把 点叠在折痕线上,得到
点叠在折痕线上,得到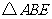 ,过
,过 点折纸片使
点折纸片使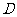 点叠在直线
点叠在直线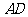 上,得折痕
上,得折痕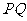 .
.
(1)求作: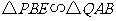 ;
;
(2)你认为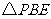 和
和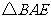 相似吗?如果相似给出证明,如不相似请说明理由;
相似吗?如果相似给出证明,如不相似请说明理由;
(3)如果沿直线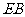 折叠纸片,过
折叠纸片,过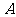 是否能叠在直线
是否能叠在直线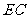 上?为什么?
上?为什么?
22.(9分)
某小区有一长100m,宽80m 空地,现将其建成花园广场,设计图案如图,阴影区域为绿化区(四块绿化区是全等的矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m,预计活动区每平方米造价60元,绿化区每平方米造价50元.
(1)设一块绿化区的长边为 x m,写出工程总造价 与
与 的函数关系式(写出
的函数关系式(写出 的取值范围);
的取值范围);
 (2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出
(2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出 为整数的所有工程方案;若不能,请说明理由.(参考值
为整数的所有工程方案;若不能,请说明理由.(参考值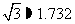 )
)
21.(9分)
在学校开展的“献爱心”活动中,小东同学打算在暑假期间帮助一家社会福利书店推销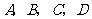 四种书刊.为了解四种书刊的销售情况,小东对五月份这四种书刊的销售量进行了统计,小东通过采集数据,绘制了两幅不完整的统计图表(如图),请你根据所给出的信息解答以下问题:
四种书刊.为了解四种书刊的销售情况,小东对五月份这四种书刊的销售量进行了统计,小东通过采集数据,绘制了两幅不完整的统计图表(如图),请你根据所给出的信息解答以下问题:
(1)填充频率分布表中的空格及补全频数分布直方图;
(2)若该书店计划订购此四种书刊6000册,请你计算 种书刊应采购多少册较合适?
种书刊应采购多少册较合适?
(3)针对调查结果;请你帮助小东同学给该书店一条合理化的建议.
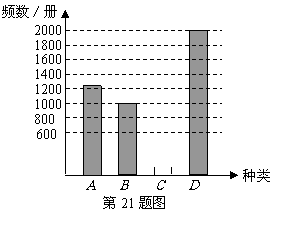 频率分布表
频率分布表
|
书刊种类 |
频数 |
频率 |
|
A |
|
0.25 |
|
B |
1000 |
0.20 |
|
C |
750 |
0.15 |
|
D |
2000 |
|
20. (8分)
(8分)
如图, 为⊙O的直径,弦
为⊙O的直径,弦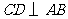 于点
于点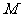 ,过
,过 点作
点作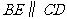 ,交
,交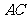 的延长线于点
的延长线于点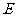 ,连接
,连接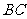 .
.
(1)求证: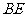 为⊙O的切线;
为⊙O的切线;
(2)如果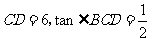 ,求⊙O的直径.
,求⊙O的直径.
19.(8分)
先化简,再求值: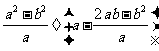 ,其中
,其中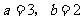 .
.
18.甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是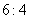 ,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是
.
,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com