
3.已知不等边三角形的一边等于5,另一边等于3,若第三边长为奇数,则周长等于
A.13 8.11 C.11,13或15 D.15
2.不等式组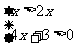 的解集为
的解集为
A.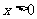 B.
B.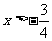 C.
C.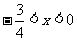 D.
D.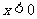
1.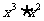 的运算结果是
的运算结果是
A.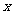 B.
B.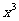 C.
C.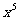 D.
D.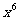
27.(本题满分l0分)
如图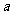 ,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE。
,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE。
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图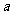 中的△CEF绕点C旋转一定的角度,得到图
中的△CEF绕点C旋转一定的角度,得到图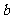 ,(1)中的结论还成立吗?做出判断并说明理由;
,(1)中的结论还成立吗?做出判断并说明理由;
(3)若将图a中的△ABC绕点C旋转一定的角度,请你画出一个变换后的图形C(草图即可),(1)中的结论还成立吗?做出判断不必说明理由;
(4)根据以上证明、说理、画图,归纳你的发现。
26.(本题满分8分)
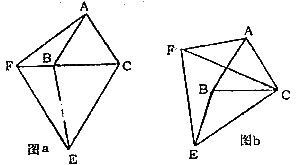
如图为临沂市滨河景观一处石拱桥,三孔桥横截面的三个孔都呈抛物线形。两小孔形状、大小都相同。正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(即NC=4.5米)。当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF。
25.(本题满分8分)
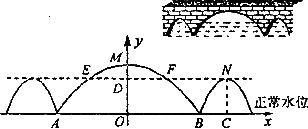
如图,Rt△ABC中,∠C=90º,∠B的平分线交AC于E,DE⊥BE。
(1)试说明AC是ABED外接圆的切线;
(2)若CE=1,BC=2,求BD。
23.证明(本题满分8分)
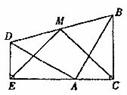
两个全等的含30º,60º的三角板ADE和三角板ABC如图所示放置。E、A、C三点在一条直线上,连结BD,取BD的中点M,连结ME、MC。试判断△EMC的形状,并说明理由。
22.计算(本题满分8分)
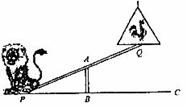
马戏团让狮子和公鸡表演跷跷板节目。跷跷板支柱 AB的高度为1.2米。
(1)若吊环高度为2米,支点A为跷跷板PQ的中点.狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米。在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ的什么位置时。狮子刚好能将公鸡送到吊环上?
21.(本题满分8分)
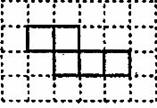
马小虎准备制作一个封闭的正方体盒子。他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分)。经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子。(添加所有符合要求的正方形,添加的正方形用阴影表示。)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com