
5、如图:把边长为AD=10cm,AB=8cm的矩形沿着AE为折痕对折,使点D落在BC上的点F处,则DE的长为( )
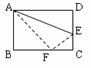
(A)3cm (B)4 cm (C)5cm (D)6cm
4、二元一次方程组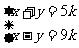 的解也是二元一次方程
的解也是二元一次方程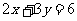 的解,则
的解,则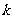 的值为:
的值为:
(A)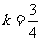 (B)
(B)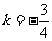 (C)
(C)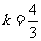 (D)
(D)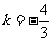
3、函数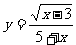 中自变量
中自变量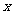 的取值范围是( )
的取值范围是( )
(A)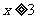 (B)
(B)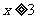 且
且 (C)
(C) (D)
(D) 且
且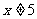
2、点A(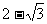 ,
,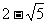 )在( )
)在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
1、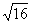 的算术平方根是( )
的算术平方根是( )
(A) (B)2 (C)
(B)2 (C) (D)4
(D)4
29.(本题12分)一次函数y=kx+k过点(1,4)且分别与x轴,y轴交于A、B两点,
点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB
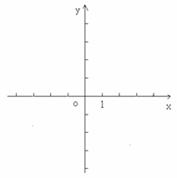
(1) 求k的值,并画出一次函数的图象
(2) 求a、b满足的等量关系式
(3) 若△APQ是等腰三角形,求△APQ的面积。
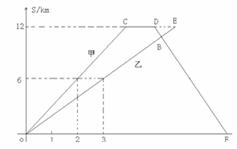
28.(本题12分)甲、乙两名同学进行登山赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:
(1)分别求出表示甲、乙两同学登山过程中路程S(km)与时间t(h)的函数关系式(不要求写出自变量t的取值范围)
(2)当甲到达山顶时,乙行进到山路上的某点A处,求A点距山顶的距离
(3)在(2)的条件下,设乙同学从A处继续登山,甲同学到达山顶后休息1h,沿原路下山,在点B处与乙相遇,此时点B与山顶距离为1.5km,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
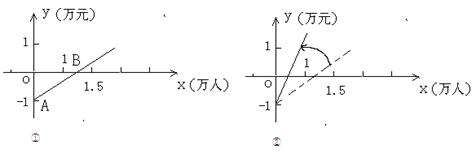
27.(本题12分)如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象。目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会。
乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏。
公交公司认为:运营成本难以下降,公司已尽力,提高票价才能扭亏。
根据这两种意见,可以把图①分别改成图②和图③。
(1)说明图①中点A和点B的实际意义。
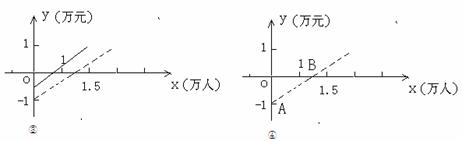
(2)你认为图②和图③两个图象中,反映乘客意见的是 ,反映公交公司意见的是 。
(3)如果公交公司采用适当提高票价又减小成本的办法实现扭亏为盈,请你在图④中画出符合这种办法的y与x的大致函数关系图象。
26.(本题10分)平行四边形两个顶点的坐标分别为(-3,0)(1,0),第3个顶点在y轴的正半轴上,且与x轴的距离为3个单位长度,求第四个顶点的坐标。
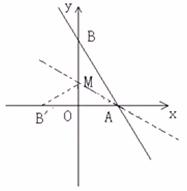
25.(本题10分)如图,直线y= -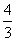 x+2与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,求直线AM的解析式。
x+2与x轴、y轴分别交于点A和点B,M是OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,求直线AM的解析式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com