
7.如果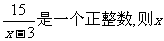 的最大的整数值为 ( )
的最大的整数值为 ( )
A.8 B.13 C.16 D.18
6.已知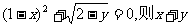 的值为 ( )
的值为 ( )
A.1 B.2 C.3 D.5
5.投掷一枚质地均匀的正六面体的骰子,掷得点数为“4”的概率为 ( )
A.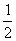 B.
B.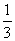 C.
C.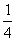 D.
D.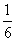
4.如图,已知⊙O中,半径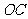 垂直于弦
垂直于弦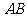 ,垂足为
,垂足为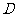 ,若
,若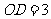 ,
,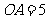 ,则
,则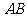 的长为
( )
的长为
( )
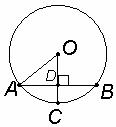
A.2 B.4 C.6 D.8
3.在图形“圆、等腰三角形,矩形、正方形”中,对称轴的条数多于一条的图形有( )
A.一个 B.两个 C.三个 D.四个
2.已知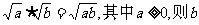 满足的条件是 ( )
满足的条件是 ( )
A.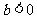 B.
B.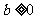 C.b必须等于零 D.不能确定
C.b必须等于零 D.不能确定
在每题的四个备选答案中只有一个是正确的,请将正确答案前的字母填在括号中。
1.已知两圆的半径分别为3、5,且它们的圆心距为2,则这两个圆的位置关系为( )
A.外离 B.内切 C.相交 D.内含
25.我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板。把两块边长为4的等边三角形板ABC和DEF叠放在一起,使三角形板DEF的顶点D与三角形板ABC的AC边中点O重合,把三角形板ABC固定不动,让三角形板EDF绕点O旋转,设射线DE与射线AB相交于点M,射线DF与线段BC 相交于点N.
(1)如图1,当射线DF经过点B,即点N与点B重合时,易证△ADM∽△CND,此时,AM·CN=
(2)将三角形板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为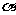 ,其中
,其中 问AM·CN的值是否改变?说明你的理由.
问AM·CN的值是否改变?说明你的理由.
(3)在(2)条件下,设AM=x,两块三角形板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
24.研究发现,二次函数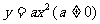 图象上任何一点到定点
图象上任何一点到定点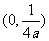 和到定直线
和到定直线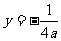 的距离相等,我们把定点
的距离相等,我们把定点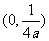 叫做抛物线
叫做抛物线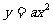 的焦点,定直线
的焦点,定直线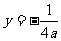 叫做抛物线
叫做抛物线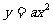 的准线.
的准线.
(1)写出函数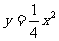 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数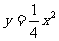 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线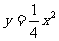 上的一个动点,F为抛物线
上的一个动点,F为抛物线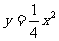 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
23.如图,Rt△ABC中,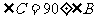 的平分线交AC与E,DE⊥BE
的平分线交AC与E,DE⊥BE
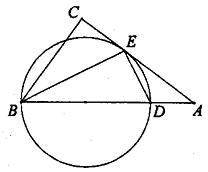
(1)试说明AC是△BED外接圆的切线;
(2)若CE=1,BC=2,求△ABC内切圆的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com