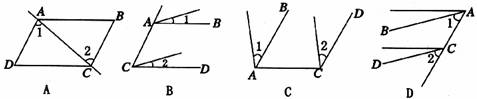
4．如下图所示，下列各图中，∠1＝∠2，能判断AB∥CD的是

3．如下图所示，AD⊥BC于D，DE∥AB，则∠1与∠2的关系是

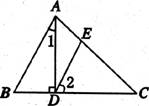
A．相等　　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．互补

C．互余　　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．关系不能确定

2．不能用一副三角板画出的角是

A．15°　　 　　　　　　　　 B．75°　　 　　　　　　　　　 C．105°　　　　　　　　　　　 D．125°

1．判断两角相等，不正确的是

A．对顶角相等

B．两直线平行，同位角相等

C．因为∠1＝∠2，∠2＝∠3，所以∠1＝∠3

D．两条直线被第三条直线所截，内错角相等

25．(本题满分12分)

如下图，设抛物线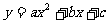与轴交于两个不同的点A(－1，0)，B(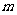，0)，与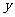轴交与点C(0，－2)，且∠ACB＝90°。

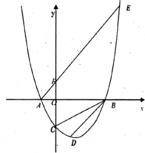
(1)求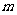的值和抛物线的解析式。

(2)已知点D(1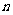，)在抛物线上，过点A的直线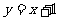交抛物线于另一点E，求点D和点E的坐标。

(3)在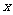轴上是否存在点P，使以点P，B，D为顶点的三角形与三角形AEB相似，若存在，请求出点P的坐标，若不存在，请说明理由。

24．(本题满分12分)

如下图，在平面直角坐标系中，A，B两点的坐标分别为A(－2，0)，B(8，0)，以AB为直径的半圆P与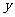轴交于点M，以AB为一边作正方形ABCD。

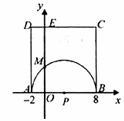
(1)求C，M两点的坐标。

(2)试判断直线CM与半圆P的位置关系，并证明你的结论。

(3)在轴上是否存在一点Q，使得△QMC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由。

23．(本题满分10分)

如下图，边长为2的等边三角形OBA的顶点A在轴的正半轴上，B点位于第二象限。将△OAB绕点O顺时针旋转30°后，得到，点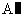恰好落在双曲线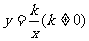上。

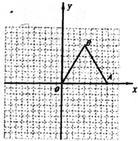
(1)在图中画出。

(2)求双曲线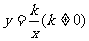的解析式。

(3)等边三角形绕着点O继续按顺时针方向旋转________度后，点再次落在双曲线上?(直接将答案填写在横线上即可，不需要说明理由)

22．(本小题满分6分)

已知：如下图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E。

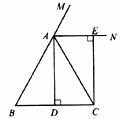
(1)求证：四边形ADCE为矩形；

(2)当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。

21．(本题满分8分)

北京至滕州高速铁路工程指挥部，要对某路段工程进行招褥，接到了甲、乙两个工程队的投标书。从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的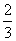；若由甲队先做10天，剩下的工程再由甲、乙两队合作30天完成。

(1)求甲、乙两队单独完成这项工程各需多少天？

(2)已知甲队每天的施工费用为8.4万元，乙队每天的施工费用为5.6万元。工程预算的施工费用为500万元．为缩短工期并高效完成工程，拟安排预算的施工费用是否够用？若不够用，需追加 预算多少万元？请给出你的判断并说明理由．

20．(本题满分6分)

水果种植大户小方，为了吸引更多的顾客，组织了观光采摘游活动。每一位来采摘水果的顾客都有一次抽奖机会：在一只不透明的盒子里有A、B、C、D四张外形完全相同的卡片，抽奖时先随机抽出一张卡片，再从盒子中剩下的3张中抽取第二张。

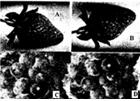
(1)请你利用树状图(或列表)的方法，表示前后两次抽得酌卡片所有可能的情况。

(2)如果抽得的两张卡片是同一种水果图片就可获得奖励，那么得到奖励的概率是多少？