4、 医学研究发现一种新病毒的直径约为0．000043毫米，则这个数用科学记数法表示为 ( 　　)

A．0．43×10^-4　　 　　　 B．0．43×10⁴ 　　　　　 C．4．3×10^-5 　　　 D．0．43×105

3、下列各组数中，以a、b、c为边的三角形不是直角三角形的是 ( 　)

A、a=1．5，b=2，c=3　　 　　　　 B、a=7，b=24，c =25

C、a=6，b=8，c =10 　　　　　　　　 D、a =3，b=4，c=5

2、己知双曲线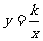(k≠0)经过点(3，1)，则它还经过点 (　 　)

A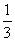．(，-9)　 　　　　　 B．(-1，3)　 　　　　　　 C．(-1，-3)　 　　 D．(6，)

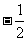1、在式子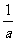、、、、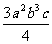、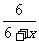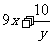中，分式的个数有(　 )

A、2个　　 　　　　　　　　 B、3个　　 　　　　　　　　 C、4个　　　　　　　　 D、5个

24．(本题12分)

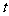一天早上6点钟汪老师从学校出发乘车去市里开会，8点准时到会场，中午12点钟回到学校，他这一段时间内的行程(km)(即离开学校的距离)与时间(h)的关系可用下图所示的折线表示，根据下图提供的有关信息，解答下列问题：

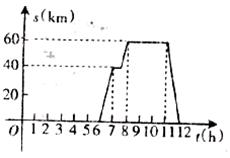
(1)开会地点离学校多远？

(2)求出汪老师在返校途中路程(km)与时间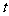(h)的函数关系式；

(3)请你用一段简短的话，对汪老师从早上6点到中午12点的活动情况进行描述。

23．(本题12分)

在某张航海图上，标明了三个观测点的坐标为O(0，0)，B(12，0)，C(12，16)，由三个观测点确定的圆形区域是海洋生物保护区，如下图所示。

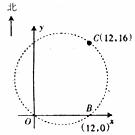
(1)求圆形区域的面积(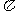取3.14)；

(2)某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，请作图确定A点的位置，并求观测点B到渔船A的距离(结果保留三个有效数字)；

(3)请直接判断并写出如果渔船A继续向西航行，能否闯入保护区。

22．(本题12分)

如下图，在以O为圆心的两个同心圆中，小圆的半径为2，大圆的弦AB与小圆交于点C、D，AC＝CD，且∠DOC＝60°。

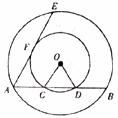
(1)求大圆的半径；

(2)若大圆的弦AE与小圆切于点F，求AE的长。

21．(本题10分)

某校教学楼后面紧邻一个土坡，坡上面是一块平地，如下图所示，BC∥AD，斜坡AB的长为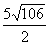米，坡度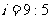。为了防止山体滑坡，保障安全，学校决定对该土坡进行改造，地质人员堪测，当坡角不超过45°时，可确保山体不滑坡。

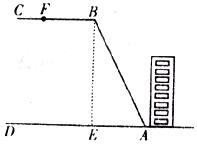
(1)求改造前坡顶B到地面的垂直距离BE的长；

(2)为确保安全，学校计划改造时保持坡脚A不动，坡顶B沿BC前进到F处，问BF至少是多少米？

20．(本题10分)

如下图，在Rt△ABC中，∠C＝90°，∠A＝60°，点E、F分别在AB、AC上，把点A沿着EF对折，使点A落在BC上点D处，且使ED⊥BC。

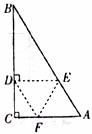
(1)猜测AE与BE的数量关系，并说明理由；

(2)求证：四边形AEDF是菱形。

19．(本题8分)

解不等式组，并把其解集在数轴上表示出来：