31．如下图，在□ABCD中，AB⊥AC，对角线BD，AC相交于点O，将直线AC绕着点O顺时针旋转，分别交BE，AD于点E、F。

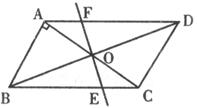
(1)证明：当旋转角为90°时，四边形ABEF是平行四边形；

(2)请你探索在旋转过程中，线段AF与CE的数量关系，并给出证明；

(3)若AB＝1，BC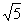＝，在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求此时AC绕点O顺时针旋转的度数。

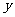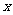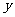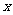30．为预防“甲型H1N1流感”，某校对教室进行“药熏消毒”。已知药物燃烧阶段，室内每立方米空气中的含药量(毫克)与燃烧时间(分钟)成正比例；燃烧结束后，与成反比例(如下图所示)，现测得药物10分钟燃烧完，此时教室内每立方米空气中含药量为8毫克。

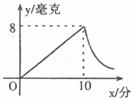
请根据以上信息解答下列问题：

(1)求药物燃烧时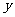与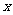的函数表达式；

(2)求药物燃烧结束后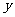与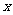的函数表达式；

(3)如果当每立方米空气中含药量低于1.6毫克时，才能对人体无毒害作用，那么从消毒开始，经多长时间学生才可以回教室？

29．袋中装有质地、大小相同的红球、蓝球、白球各一个，摇匀后从中摸出一个球，然后放回，摇匀后再摸出一个球。

(1)请你用列表的方法或画树状圈的方法分析两次摸出的球的所有结果；

(2)求出两次摸出颜色相同的球的概率。

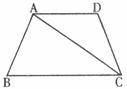
28．如下图，在等腰梯形ABCD中，AB＝CD，∠D＝120°，AC平分∠BCD，梯形的中位线长为6，求AC的长及梯形的面积。

27．若函数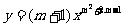是反比例函数，且它的图像位于第一、三象限内，求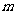的值。

26．解方程：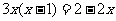

25．已知点A是函数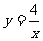的图像上的一点，AB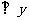轴于点B，O为原点，则△AOB面积是__________。

24．两个装有乒乓球的盒子，其中一个装有2个白球，1个黄球；另一个装有1个白球，2个黄球。现从这两个盒中随机各抽取一个球，则取出的两个球一个是白球一个是黄球的概率是__________。

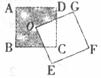
23．如下图，正方形ABCD和正方形OEFG的边长均为4，O为正方形ABCD的中心，则图中阴影部分的面积是__________。

22．若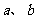是方程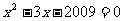的两个根，则代数式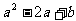的值为__________。