23．已知如图1所示，在等边△ABC和等边△ADE中，点B、A、D在一条直线上，BE、CD交于F.

⑴求证：△≌△.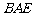

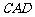⑵求∠BFC的大小.

⑶在图1的基础上，将△ADE绕点A按顺时针方向旋转180°，此时BE交CD的延长线于点F，其他条件不变，得到图2所示的图形,请直接写出⑴、⑵中结论是否仍然成立.

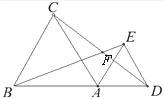
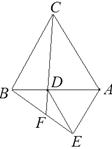
　　　　 　　　　　　　　　　 　　　　图1　　　　 　　　　　　　　　　　 图2

22．大家知道，因式分解是代数中一种重要的恒等变形.应用因式分解的思想方法有时能取得意想不到的效果，如化简：

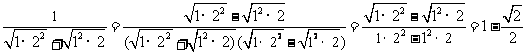
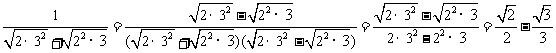
⑴从以上化简的结果中找出规律，直接写出用n(n是正整数)表示上面规律的式子.

⑵根据以上规律，计算

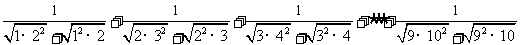
21．已知关于x的方程(*)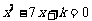

　　 ⑴请你选择一个合适的整数k，使得到的方程有两个不相等的实数根，并说明它的正确性.

⑵如果方程(*)的两个实数根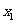,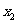的值恰好是一个菱形的两条对角线长且满足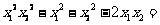95。求该菱形的面积.

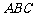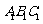20．在平面直角坐标系中，每个小方格都是边长为1的正方形，有△和△，其位置如图所示，

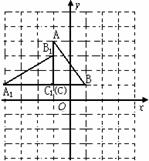
⑴将△ABC绕C点，按时针方向旋转时与△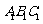重合(直接填在横线上)

⑵在图中作出△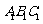关于原点O对称的△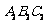(不写作法)

⑶若将△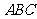先向右平移2个单位，再向下平移2个单位后，只通过一次旋转变换就能与△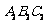重合吗？若能，请直接指出旋转中心的坐标、方向及旋转角的度数，若不能，请说明理由.

19．如图⑴所示，现有边长为1的等边三角形黑色小瓷砖若干块.利用这些小瓷砖在⑵、⑶、⑷网格中(每个小等边三角形的边长均是1)可拼出一些美丽的图形.

请你分别在⑶、⑷网格中各画一种与⑵不同的拼法.

要求：①所画拼法中有一种是中心对称图形，另一种既是轴对称又是中心对称图形；

②所画小瓷砖块数不限，但都必须和网格中小三角形重合.

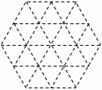
⑴　　　　　 　⑵　　　　　　　 ⑶　　　　　　 ⑷

18．用适当的方法解下列方程.

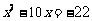　　　 ⑴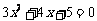　 ⑵　　　　　　　 ⑶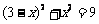

17．计算：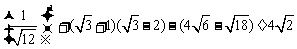

16．已知x，y均是正整数，且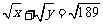，则的值为___________．

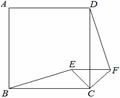
15．如图所示，点E是正方形ABCD内任一点，把△BEC绕点C旋转至△DFC的位置，∠CFE=_________.

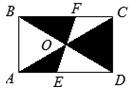
14．如图所示，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=3，BC=4，则图中阴影部分的面积为___________.