
3.关于x的一元二次方程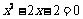 的根的情况是( )
的根的情况是( )
A.有两个同号实数根 B.有两个异号实数根
C.有两个相等的实数根 D.没有实数根
2.若abc<0,则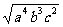 可能化简的结果为( )
可能化简的结果为( )
①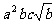 ②
②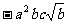 ③
③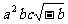 ④
④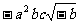
A.①或② B.③或④ C. ①或③ D.②或④
1.下列计算正确的是( )
A.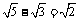 B.
B.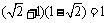
C.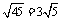 D.
D.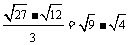
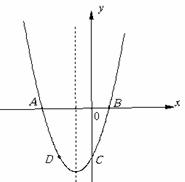
26.已知:二次函数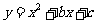 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.
25.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数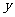 (亩)与补贴数额
(亩)与补贴数额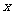 (元)之间大致满足如图1所示的一次函数关系,但种植面积不超过3200亩.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系,但种植面积不超过3200亩.随着补贴数额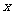 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益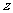 (元)会相应降低,且
(元)会相应降低,且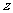 与
与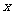 之间也大致满足如图2所示的一次函数关系,且每亩收益不低于1800元.
之间也大致满足如图2所示的一次函数关系,且每亩收益不低于1800元.
(1)分别求出政府补贴政策实施后,种植亩数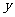 和每亩蔬菜的收益
和每亩蔬菜的收益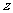 与政府补贴数额
与政府补贴数额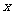 之间的函数关系式;
之间的函数关系式;
(2)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益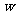 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额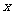 定为多少?并求出总收益
定为多少?并求出总收益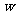 的最大值.
的最大值.
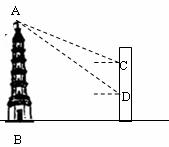
24.如图,已知大楼的每层高为3米,小明家住在第12层,某天,小明在自家阳台C处观测对面的一座古塔,此时观测到塔顶A的仰角为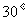 ,他为了测量此塔的高度,于是下到住在同一单元第9层的同学小亮家的阳台D处又测得塔顶A的仰角为
,他为了测量此塔的高度,于是下到住在同一单元第9层的同学小亮家的阳台D处又测得塔顶A的仰角为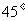 ,请你帮他算算这座塔有多高?(小明的身高忽略不计,塔底与楼底在同一水平面上)(结果精确到0.1米,
,请你帮他算算这座塔有多高?(小明的身高忽略不计,塔底与楼底在同一水平面上)(结果精确到0.1米,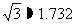 )
)
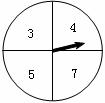
23.有一个可以自由转动的转盘,被分成了4个相同的扇形,分别标有数3、4、5、7(如图所示),另有一个不透明的口袋装有分别标有数0、1、3的三个小球(除数不同外,其余都相同)。小李转动一次转盘,停止后指针指向某一扇形(如果指针恰好指在分割线上,那么重转一次),用扇形内的数作为被减数,小张任意摸出一个小球,用小球上的数作为减数,然后计算这两个数的差。
(1)请你用画树状图或列表的方法,求这两个数的差为4的概率;
(2)小李与小张做游戏,规则是:若这两个数的差为奇数,小李赢;否则,小张赢。你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平。
22.已知:二次函数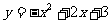
(1)求函数图象的顶点P的坐标;
(2)设函数图象与y轴交于点C,与x轴交于点A、B(点A在点B的左侧),求点A、B、C的坐标;
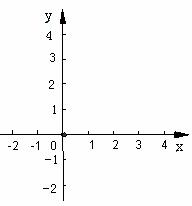
(3)根据对称轴、点P、A、B、C的坐标,在如图所示的坐标系内,画出二次函数的示意图,并求出△PBC的面积.
21.某水果批发商经销一种高档水果,如果每千克赢利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商场要保证每天赢利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?

20.先化简,再求值: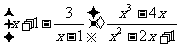 ,其中
,其中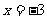 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com