
4.从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为 ( )
A.432 B.288 C.216 D.108
3.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 ( )
A.9 B.18 C.27 D.36
2.若正方体的棱长为 ,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
A. 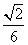 B.
B.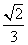 C
.
C
.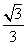 D.
D. 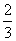
1.设集合A={4,5,7,9},B={3,4,7,8,9},全集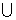 =A
=A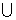 B,则集合
B,则集合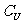 (A
(A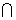 B)中的元素共有 ( )
B)中的元素共有 ( )
A.3个 B. 4个 C. 5个 D. 6个
22.(本小题满分12分)
已知函数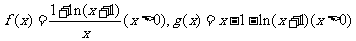
(Ⅰ)判断函数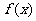 的单调性并证明你的结论.
的单调性并证明你的结论.
(Ⅱ)设方程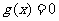 的根为
的根为 ,且
,且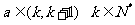 ,求正整数
,求正整数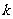 的值.
的值.
(Ⅲ)若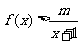 恒成立,求整数m的最大值.
恒成立,求整数m的最大值.
(Ⅳ)附加题
求证:(1+1×2)(1+2×3)(1+3×4)……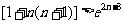
(注:附加题5分,不计入总分)
21.(本小题满分12分)
已知数列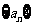 ,
,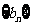 满足
满足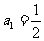 ,
,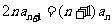 且
且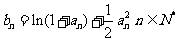
(Ⅰ)求数列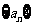 的通项公式.
的通项公式.
(Ⅱ)对一切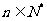 ,证明不等式
,证明不等式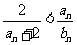 成立.
成立.
(Ⅲ)设数列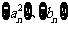 的前n项和分别为
的前n项和分别为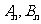 证明:
证明: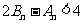
20.(本小题满分12分)
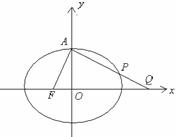
设椭圆C: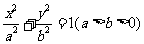 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C于点P,交
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C于点P,交 轴正半轴于点Q,且
轴正半轴于点Q,且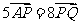 .
.
(Ⅰ)求椭圆的离心率.
(Ⅱ)若过A、Q、F三点的圆恰好与直线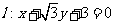 相切,求椭圆C的方程
相切,求椭圆C的方程
19.(本小题满分12分)
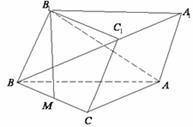
如图斜三棱椎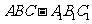 的底面是直角三角形,
的底面是直角三角形,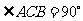 ,点
,点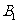 在底面ABC上的射影M恰好是BC的中点,且
在底面ABC上的射影M恰好是BC的中点,且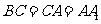 .
.
(Ⅰ)求证:平面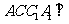 平面
平面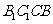
(Ⅱ)求证: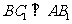
(Ⅲ)求二面角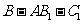 的大小
的大小
18.(本小题满分12分)
某教室用4盏灯照明,每盏灯各使用节能灯管一只,且型号相同,假定每盏灯能否正常照明只与灯管的寿命有关,该型号的灯管寿命为1年以上的概率为0.8,寿命为2年以上的概率为0.3,从使用之日起,每满一年进行一次灯管更换工作,只更换已坏的灯管,平时不换。
(Ⅰ)在第一次灯管更换工作中,求不需要换灯管的概率。
(Ⅱ)在第二次灯管更换工作中,对其中的某盏灯来说,求该盏灯需要更换灯管的概率
(Ⅲ)在第二次灯管更换工作中,该教室需更换灯管的只数为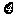 ,求
,求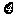 的分布列和数学期望.
的分布列和数学期望.
17.(本小题满分10分)已知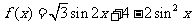
(Ⅰ)求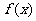 的最小正周期和单调递减区间。
的最小正周期和单调递减区间。
(Ⅱ)在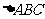 中,
中,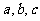 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若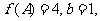
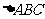 的面积是
的面积是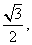 求
求 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com