
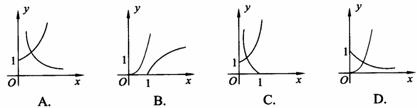
4.已知函数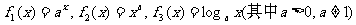 在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是 ( )
在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是 ( )
3.给出如下三个命题:①四个实数a、b、c、d依次成等比数列的必要而不充分条件是ad=bc;②命题“若x≥2且y≥3,则x+y≥5”为假命题;③若p∧q为假命题,则p、q均为假命题. 其中不正确的命题序号是 ( )
A.①②③ B.①② C.②③ D.③
2.若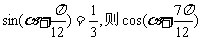 的值为 ( )
的值为 ( )
A.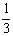 B.
B.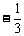 C.
C.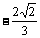 D.
D.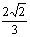
1.已知集合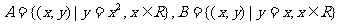 ,则集合
,则集合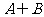 中的元素个数为 ( )
中的元素个数为 ( )
A.0个 B.1个 C.2个 D.无穷多个
22.(14分)
已知直线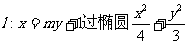 =1的右焦点F,且交椭圆于A、B两点,点A、B在直线g :
x=4上的射影为D、E.
=1的右焦点F,且交椭圆于A、B两点,点A、B在直线g :
x=4上的射影为D、E.
(I)若直线l交y轴于点M,且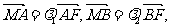 当m变化时,求
当m变化时,求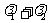 的值;
的值;
(II)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一点是N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
21.(12分)
|
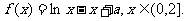
(I)求 的单调区间;
的单调区间;
(II)若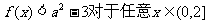 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
20.(12分)
已知
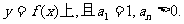
(I)求数列{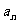 }的通项公式
}的通项公式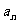 ;
;
(II)数列{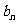 }的首项b1=1,前n项和为Tn,且
}的首项b1=1,前n项和为Tn,且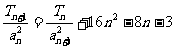 ,求数列{
,求数列{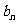 }的通项公式bn.
}的通项公式bn.
19.(12分)
某渔业公司年初用98万元购进一艘渔船用于捕捞,第一年需各种费用12万元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的总收入为50万元.
(I)该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)?
(II)该船捕捞若干年后,处理方案有两种:①当年平均盈利达到最大值时,以26万元的价格卖出;②当盈利总额达到最大值时,以10万元的价格卖出. 问哪一种方案较为合算,请说明理由.
18.(12分)
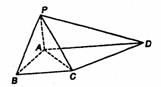
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=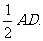
(I)求证:平面PAC⊥平面PCD;
(II)在棱PD上是否存在一点E,使CE∥平面PAB?若存在,请确定E点的位置;若不存在,请说明理由.
17.(12分)
已知△ABC的面积S满足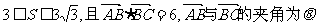
(I)求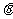 的取值范围;
的取值范围;
(2)求函数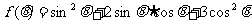 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com