
21.(本小题满分14分)已知数列{an}满足a1=1,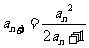 (n
(n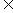 N*).
N*).
(1)求a2 , a3的值;
(2)求数列{an}的通项公式;
(3)求证: .
.
20.(本小题满分14分)
已知函数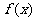 =
=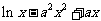 (a
(a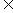 R).
R).
(1)当 时,证明函数
时,证明函数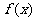 只有一个零点;
只有一个零点;
(2)若函数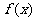 在区间(1,+
在区间(1,+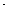 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
19.(本小题满分14分)
(1)椭圆C: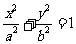 (a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、 PB分别与y轴交于点M、N,求证:
(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、 PB分别与y轴交于点M、N,求证: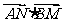 为定值
为定值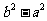 .
.
(2)由(1)类比可得如下真命题:双曲线C: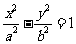 (a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证: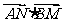 为定值.请写出这个定值(不要求给出解题过程).
为定值.请写出这个定值(不要求给出解题过程).
18.(本小题满分12分)
某工厂生产甲、乙两种产品,每生产一吨产品所消耗的电能和煤、所需工人人数以及所得产值如下表所示:
|
品种 |
电能(千度) |
煤(吨) |
工人人数(人) |
产值(万元) |
|
甲 |
2 |
3 |
5 |
7 |
|
乙 |
8 |
5 |
2 |
10 |
已知该工厂的工人人数最多是200人,根据限额,该工厂每天消耗电能不得超过160千度,消耗煤不得超过150吨,问怎样安排甲、乙两种产品的生产数量,才能使每天所得的产值最大.
17.(本小题满分14分)
如图3所示,在三棱锥P-ABC中,PA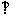 平面ABC,AB=BC=CA=2, M为AB的中点,四点P、A、M、C都在球O的球面上.
平面ABC,AB=BC=CA=2, M为AB的中点,四点P、A、M、C都在球O的球面上.
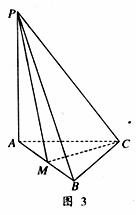
(1)证明:平面PAB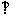 平面PCM;
平面PCM;
(2)证明:线段PC的中点为球O的球心;
(3)若球O的表面积为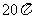 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值.
16.(本小题满分12分)
已知点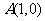 ,
,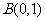 ,
,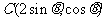 .
.
(1)若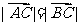 ,求tan
,求tan 的值;
的值;
(2)若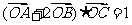 ,其中O为坐标原点,求sin2
,其中O为坐标原点,求sin2 的值.
的值.
(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分.
13.(坐标系与参数方程)已知圆C的参数方程为
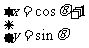 (
( 为参数),则点P (4, 4) 与圆C上的点的最远距离是_________.
为参数),则点P (4, 4) 与圆C上的点的最远距离是_________.
14.(不等式选讲)不等式 的解集是__________.
的解集是__________.
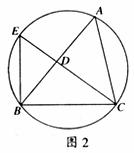
15.(几何证明选讲)如图2所示,圆内接 ABC的
ABC的 C的平分线CD 延长后交圆于点E,连接BE,己知BD=3,CE=7,BC=5,则线段 BE=__________.
C的平分线CD 延长后交圆于点E,连接BE,己知BD=3,CE=7,BC=5,则线段 BE=__________.
(一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.
9. 函数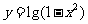 的定义域是_________.
的定义域是_________.
10.在复平面内,复数1+i与-1+3i分别对应向量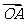 与
与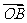 ,其中O为坐标原点,则
,其中O为坐标原点,则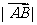 =_________.
=_________.
11.在一次数学测试(满分为150分)中,某地区10000名考生的分数X服从正态分布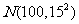 ,据统计,分数在110分以上的考生共2514人,则分数在90分以上的考生共________人.
,据统计,分数在110分以上的考生共2514人,则分数在90分以上的考生共________人.
12.已知a为正常数,定义运算“×”,如下:对任意m,n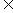 N*,若m×n=a,则(m+1) ×n=2a,m×(n+1)=a+1.当1×1=1时,则1×10=______,5×10=________.
N*,若m×n=a,则(m+1) ×n=2a,m×(n+1)=a+1.当1×1=1时,则1×10=______,5×10=________.
8.甲、乙两位同学玩游戏,对于给定的实数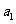 ,按下列方法操作一次产生一个新的实数: 由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数: 由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把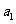 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把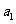 除以2后再加上12,这样就可得到一个新的实数
除以2后再加上12,这样就可得到一个新的实数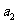 .对实数
.对实数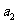 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数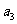 .当
.当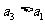 时,甲获胜,否则乙获胜.若甲获胜的概率为
时,甲获胜,否则乙获胜.若甲获胜的概率为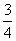 ,则
,则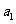 的取值范围是
的取值范围是
A.( ,12) B.[ 24, +
,12) B.[ 24, + ]
]
C.(12,24) D.( ,12]
,12]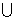 [24,+
[24,+  )
)
7.某班星期二的课表有6节课,其中上午4节,下午2节,要排语文、数学、英语、信息技术、体育、地理各1节,要求上午第一节课不排体育,数学必须排在上午,则不同排法种数共有 ( )
A.600种 B.480种 C.408种 D.384种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com