
1.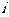 是虚数单位,
是虚数单位,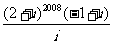 的虚部是 ( )
的虚部是 ( )
A.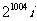 B.
B.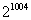 C.
C. D.
D.
22.(本小题满分12分)已知函数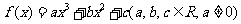 的图象过
的图象过
点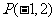 ,且在点
,且在点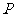 处的切线与直线
处的切线与直线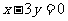 垂直.
垂直.
(1)若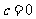 ,试求函数
,试求函数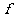 (
(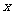 ) 的单调区间;
) 的单调区间;
(2)若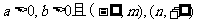 是
是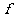 (
(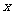 ) 的递增区间,求
) 的递增区间,求 的取值范围.
的取值范围.
21.(本小题满分12分)在平面直角坐标系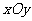 中,已知圆
中,已知圆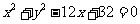 的圆心为
的圆心为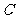 ,过点
,过点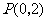 且斜率为
且斜率为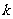 的直线与圆
的直线与圆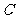 相交于不同的两点
相交于不同的两点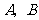 .
.
(1)求圆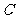 的圆心坐标、半径大小,并求
的圆心坐标、半径大小,并求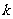 的取值范围;
的取值范围;
(2)是否存在常数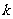 ,使得向量
,使得向量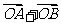 与
与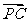 共线?如果存在,求
共线?如果存在,求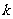 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
20.(本小题满分12分)在数列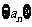 中,
中,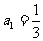 ,并且对于任意
,并且对于任意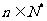 ,且
,且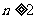 ,都有
,都有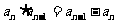 成立,令
成立,令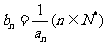 .
.
(1)求证数列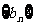 是等差数列,求数列
是等差数列,求数列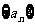 的通项公式;
的通项公式;
(2)设数列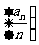 的前n项和为
的前n项和为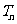 ,证明:
,证明: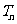 <
<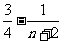 .
.
19.(本小题满分12分)直三棱柱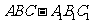 中,
中,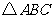 为等腰直角三角形,
为等腰直角三角形,
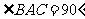 ,且
,且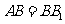 ,
,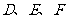 分别是
分别是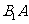 、
、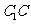 、
、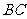 的中点.
的中点.
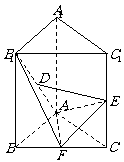

⑴求证: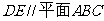 ;
;
⑵求二面角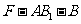 的正切值 ;
的正切值 ;
⑶求证: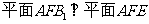 .
.
18.(本小题满分13分)在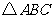 中,已知内角
中,已知内角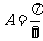 ,边
,边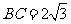 .设内角
.设内角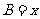 ,周长为
,周长为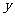 .
.
(1)求函数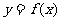 的解析式和定义域;
的解析式和定义域;
(2)求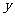 的最大值.
的最大值.
17.(本小题满分13分)某商场经销商品,顾客可采用一次性付款或分期付款购买,
根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
①求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
②求3位顾客每人购买1件该商品,商场获得利润不超过650的概率.
16.有下列命题:①在函数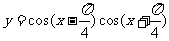 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为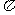 ;②函数
;②函数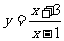 的图象关于点
的图象关于点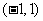 对称;③关于
对称;③关于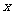 的方程
的方程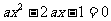 有且仅有一个实数根,则实数
有且仅有一个实数根,则实数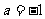 ;④已知命题p:对任意的
;④已知命题p:对任意的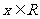 ,都有
,都有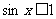 ,则
,则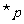 是:存在
是:存在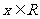 ,使得
,使得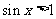 .其中所有真命题的序号是_______.
.其中所有真命题的序号是_______.
15.设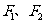 分别是椭圆
分别是椭圆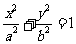 (
(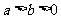 )的左、右焦点,
)的左、右焦点,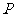 是其右准线上纵坐标为
是其右准线上纵坐标为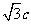 (
(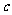 为半焦距)的点,且
为半焦距)的点,且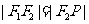 ,则椭圆的离心率是 .
,则椭圆的离心率是 .
14.在正方体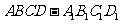 中,
中,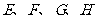 分别是边
分别是边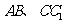 、
、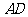 、
、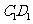 的中点,则直线
的中点,则直线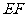 与直线
与直线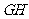 所成角的余弦值为_______.
所成角的余弦值为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com