22．B(本小题满分10分)选修4－4：坐标系与参数方程已知圆系的方程为

x²+y²-2axCos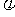-2aySin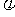=0(a>0)

　 (1)求圆系圆心的轨迹方程;

　 (2)证明圆心轨迹与动圆相交所得的公共弦长为定值;

22．A．(本小题满分10分)选修4－1：几何证明选讲

如图所示，已知⊙O₁与⊙O₂相交于A，B两点，过点A作⊙O₁的切线交⊙O₂于点C，过点B作两圆的割线，分别交⊙O₁，⊙O₂于点D，E，DE与AC相交于点P.

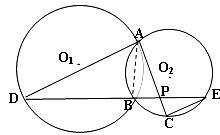
　 (1)求证：AD∥EC；

　 (2)若AD是⊙O₂的切线,且PA=6,PC=2,BD=9,求AD的长;

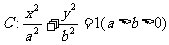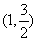21．(本小题满分12分)已知椭圆过点，且离心率。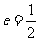

　 (1)求椭圆方程；

　 (2)若直线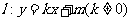与椭圆交于不同的两点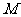、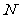，且线段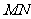的垂直平分线过定点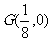，求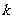的取值范围。

20．(本小题满分12分)数列{a_n}的前n项和为S_n,a₁=1,a_n+1=2S_n(n∈N^*)．

　 (1)求数列{a_n}的通项a_n；

　 (2)求数列{na_n}的前n项和T_n．

19．(本小题满分12分)设函数f(x)=tx²+2t²x+t-1(x∈R,t>0)．

　 (1)求f(x)的最小值h(t)；

　 (2)若h(t)<-2t+m对t∈(0,2)恒成立，求实数m的取值范围．

18．(本小题满分12分)如图，在底面是正方形的四棱锥P-ABCD中，PA=AC=2，PB=PD=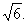

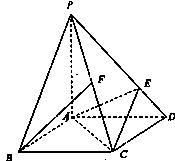
　 (1)证明PA⊥平面ABCD；

　 (2)已知点E在PD上，且PE:ED=2:1，点F为棱PC的中点，证明BF//平面AEC。

　 (3)求四面体FACD的体积;

17．(本小题满分12分)在△ABC中，tanA=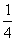，tanB=．

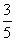　 (1)求角C的大小；

　 (2)若AB边的长为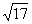，求BC边的长．

16．设函数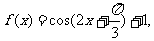有以下结论：

①点(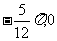)是函数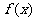图象的一个对称中心；

②直线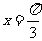是函数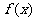图象的一条对称轴；

③函数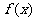的最小正周期是；

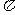④将函数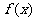的图象向右平移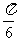个单位后，对应的函数是偶函数。

其中所有正确结论的序号是　　　　　　　 。

15．已知定点A(4，2)，O是坐标原点，P是线段OA的垂直平分线 上一点，若∠OPA为钝角，那么点P的横坐标的取值范围是　　　　　　 。

14．已知曲线y=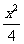-3lnx的一条切线的斜率为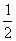，则切点的坐标为________.