
6.把5本不同的书全部分给3名同学,每人至少一本,则不同分法的种数有 ( )
A.210 B.200 C.150 D.120
5.若弧度是2的圆心角所对的弦长为2,则这个圆心角所夹扇形的面积是 ( )
A.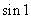 B.
B.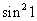 C.
C. 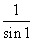 D.
D.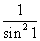
4.已知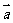 、
、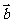 均为非零向量,命题p:
均为非零向量,命题p: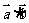 >0,命题q:
>0,命题q: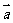 与
与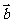 的夹角为锐角,则p是q成立的 ( )
的夹角为锐角,则p是q成立的 ( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
3.在等比数列{an}中,若a1+a2=20,a3+a4=40则数列{an}的前6项和S6= ( )
A.120 B.140 C. 160 D.180
2.设 ,则a与b的大小关系是 ( )
,则a与b的大小关系是 ( )
A.a>b B.a<b C.a=b D.a≤b
1.函数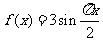 的最小正周期是 ( )
的最小正周期是 ( )
A.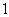 B.
B.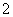 C.
C.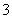 D.
D. 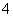
22.(本小题满分15分)定义: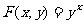 (
(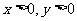 )
)
(1)设函数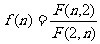
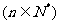 ,求函数
,求函数 的最小值;
的最小值;
(2)解关于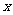 的不等式:
的不等式: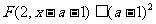
(3)设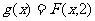 ,正项数列
,正项数列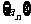 满足:
满足: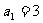 ,
,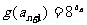 ;求数列
;求数列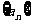 的通项公式,并求所有可能乘积
的通项公式,并求所有可能乘积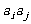 (
(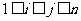 )的和。
)的和。
21.(本小题满分15分) 已知函数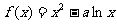 在
在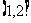 是增函数,
是增函数,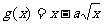 在
在 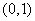 是减函数;
是减函数;
(1)求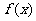 、
、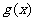 的表达式;
的表达式;
(2)求证:当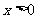 时,方程
时,方程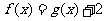 有唯一解;
有唯一解;
(3)当 时,若
时,若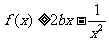 在
在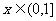 内恒成立,求
内恒成立,求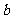 的取值范围;
的取值范围;
20.(本小题满分14分)已知椭圆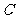 的焦点在
的焦点在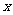 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线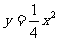 的焦点,离心率等于
的焦点,离心率等于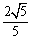 .
.
(1)求椭圆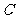 的方程;
的方程;
(2)过椭圆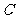 的右焦点
的右焦点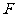 作直线
作直线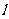 交椭圆
交椭圆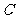 于
于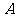 、
、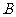 两点,交
两点,交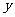 轴于点
轴于点 .若
.若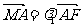 ,
,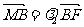 ,求证:
,求证: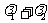 为定值.
为定值.
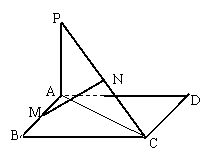
19.(本小题满分14分)如图,已知矩形ABCD,PA⊥平面AC于点A,M、N分别是AB、PC的中点.
(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD所成的二面角为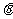 ,能否确定
,能否确定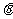 ,使得直线MN是异面直线AB与PC的公垂线?若能确定,求出
,使得直线MN是异面直线AB与PC的公垂线?若能确定,求出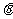 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com