
20.(本大题满分13分)
已知数列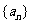 满足:
满足: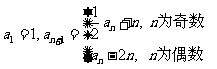 ,且
,且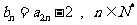
(Ⅰ)求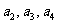 ;
;
(Ⅱ)求证:数列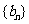 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(Ⅲ)在(Ⅱ)情形下,设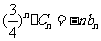 ,设
,设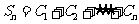 ,求证:
,求证: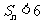 .
.
19.本大题满分12分)
已知函数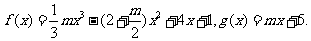
(Ⅰ)当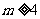 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)是否存在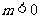 ,使得对任意的
,使得对任意的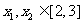 都有
都有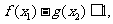 若存在,求
若存在,求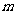 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
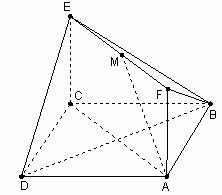
18.(本大题满分12分)
如图,已知正方形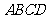 和矩形
和矩形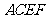 所在的平面互相垂直
所在的平面互相垂直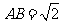 ,
,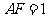 ,
,
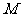 为线段
为线段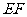 的中点。
的中点。
(Ⅰ)求证:AM∥平面BDE;
(Ⅱ)二面角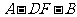 的平面角的大小.
的平面角的大小.
17.(本大题满分12分)
设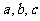 分别是先后三次抛掷一枚骰子得到的点数.
分别是先后三次抛掷一枚骰子得到的点数.
(Ⅰ)求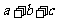 为奇数的概率;
为奇数的概率;
(Ⅱ)设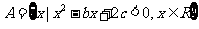 ,求
,求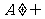 的概率.
的概率.
16.(本小题满分12分)
在△ABC中,角A、B、C所对的边分别是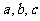 ,
,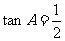 ,
,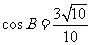 ,
,
(Ⅰ)求角C;
(Ⅱ)若△ABC的最短边长是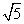 ,求最长边的长.
,求最长边的长.
15.在△OAB中,O为坐标原点,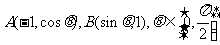 .
.
(1)若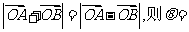 ,
,
(2)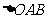 的面积最大值为
.
的面积最大值为
.
14.在等差数列 中,若
中,若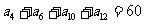 ,则
,则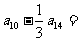 .
.
13.某学校对学生进行眼睛视力调查,采用分层抽样法抽取,该中学共有学生2000名,抽取一个容量为200的 样本,已知男生比女生多抽了10人,则该校的女生人数应是 人.
12.底面边长为2,高为1 的正四棱锥的外接球的表面积为 .
11.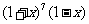 的展开式中
的展开式中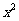 的系数是
.
的系数是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com