
1. 写出AlCl3在下列溶剂或熔液中的存在形式。
(1)在苯中 (2)在NaCl熔液中 (3)在NaF溶液中
1、写出A、B反应生成C的方程式2、推测D、E、F的结构3、F可与苯剧烈反应,写出反应的方程式
第6题(6分):回答下列问题
(1)比较下列化合物与乙醇形成氢键的能力:(H3Si)2O和(H3CH2C)2O
(2)写出 BBr3与过量NH(CH3)2在烃类溶剂中的反应。
(3)AgClO4在苯中的溶解性明显高于在烷烃中的溶解性,用Lewis酸碱性对此事实作出的解释是
第7题(10分):苯氧布洛芬钙是良好的解热镇痛消炎药,其消炎作用比阿司匹林强50 倍,是治疗慢性关节炎的首选药物。苯氧布洛芬钙(F)有多种合成方法,以下是其中一种:
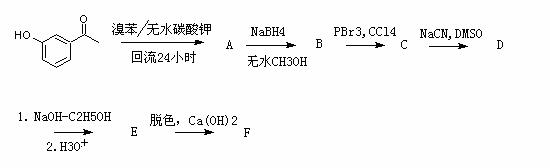
(1)写出A、B、C、D、E、F的结构简式
(2)指出A、B、C、D、E中哪些具有旋光异构体
(3)给出A的系统命名
(4)反应工艺最后一步脱色所用的物质为
第8题(9分):高性能材料纳米纤维PSB具有优良的热学、力学、光学、磁学性能而广受关注。研究者将A与对苯二甲醛溶于甲苯溶液中,N2 保护下加热回流,在沸腾的甲苯中反应5h,冷却,抽滤,干燥得到粉末状的聚合物PSB纤维。
A的结构为:

(1)试命名A__________________________ ,A中存在的离域Π键可记作
(2)写出A与对苯二甲醛发生聚合反应的方程式,并说明沸腾的甲苯对反应有何帮助?
(3)PSB具有酸致变色功能,如在HCl蒸气下,聚合物变为蓝紫色,通入NH3 聚合物又变回原来的颜色,试分析变色的机理
(4)PSB材料不但有酸致变色功能,还有光致变色功能,且变色范围十分宽广,预测其在电子工业上可能的用途___________________________________
第9题(10分):向一定量的CoCO3 中加入浓氢溴酸使之溶解,再加入浓氨水和NH4Br,搅拌下加入30%的H2O2 ,向溶液中通空气除去过量的氨气,再加浓氢溴酸到溶液为中性时开始出现红色沉淀A,A中含五种元素,其中Co为14.67%,N为17.43%,2.0gA与0.920mol/L的AgNO3溶液反应消耗16.30mLAgNO3溶液。将A过滤洗涤干燥,在110℃时加热1-2小时得到蓝紫色晶体B,失重率为4.48%,在B的冷浓溶液中加稀盐酸可以得到暗紫色晶体C,C中含Co为20.0%,含N为23.74%,A、B、C式量均不超过500,且其中N-H键键长与氨分子键长接近。
(1)通过计算,推测A、B、C的化学式
(2)写出制备A的方程式,并命名A
(3)如果事先不知道A、B、C本身的颜色,如何鉴别A、B、C三种物质?
第10题(10分):富勒烯(Fullerene)全碳分子(Cn)(n=60,70,76,84……)近年来一直是人们研究的热点。作为新发现的碳的第三种结构形式,富勒烯结构奇特新颖,具有许多激动人心的物理特性:超导、特殊的磁学性质、光电导性质以及非线性光学性质。富勒烯材料应用前景非常广泛:包括新型材料、超导、激光、红外、电化学、新型能源、天体物理、地质,甚至医学(艾滋病的防治),以C60为例,它是一个很好的超导体,M3C60(M=K、Rb、Cs)均为超导体,具有很好的电化学性质(用于制作高容量的锂电池),尤其具备奇特的光学性质。由于生成条件不同,C60分子可堆积成不同的晶体结构,如立方最密堆积和六方最密堆积结构,前者的晶胞参数a=1420pm,后者的晶胞参数a=b=1002pm,c=1639pm。
(1) 画出C60的立方最密堆积结构沿四重轴方向的投影图,用分数坐标表示出分子间多面体空隙的中心位置(每种多面体空隙只写一种即可)
(2)C60 在立方最密堆积中,离其最近的C60 分子数为多少?画出其配位多面体。
(3)C60与K+可形成组成为K3C60的超导材料,C60为立方最密堆积,K+占据什么多面体空隙?占据空隙的百分数是多少?
(4)同一温度下,C60的晶体密度为多少?若 K3C60晶胞参数a=1424pm,求 K3C60的晶体密度比C60的晶体密度增大的百分数。
第11题(10分):制金属的方法之一是电解含该金属的化合物,制备铝单质就是在加入冰晶石的条件下,高温电解Al2O3,电解化合物的前提是该化合是离子化合物,如Al2O3在高温下电解为Al3+及O2-,过去认为不可能用电解AlCl3来制铝的,但近年来,这种说法被打破,比如电解NaCl-AlCl3熔盐体系制金属铝,并取得初步研究成果。
21.已知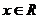 ,奇函数
,奇函数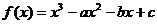 在
在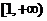 上单调.
上单调.
(Ⅰ)求字母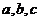 应满足的条件;
应满足的条件;
(Ⅱ)设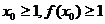 ,且满足
,且满足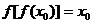 ,求证:
,求证: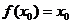 .
.
20.已知偶函数f(x)=cosqsinx-sin(x-q)+(tanq-2)sinx-sinq的最小值是0,求f(x)的最大值 及此时x的集合.
19. 设f(x)=lg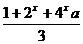 ,如果当x∈(-∞,1]时f(x)有意义,求
实数a的取值范围。
,如果当x∈(-∞,1]时f(x)有意义,求
实数a的取值范围。
18. 已知△ABC三内角A、B、C的大小成等差数列,且tanA·tanC=2+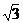 ,又知顶点C的对边c上的高等于4
,又知顶点C的对边c上的高等于4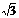 ,求△ABC的三边a、b、c及三内角。
,求△ABC的三边a、b、c及三内角。
17. 如图,AB是圆O的直径,PA垂直于圆O所在平面,C是圆周上任一点,设∠BAC=θ,PA=AB=2r,求异面直线PB和AC的距离。
16. 设等差数列{a }的前n项的和为S
}的前n项的和为S ,已知a
,已知a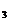 =12,S
=12,S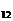 >0,S
>0,S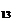 <0 。
<0 。
①.求公差d的取值范围;
②.指出S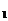 、S
、S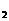 、…、S
、…、S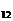 中哪一个值最大,并说明理由。(1992年全国高考)
中哪一个值最大,并说明理由。(1992年全国高考)
        P
M
A
H
B
D C
P
M
A
H
B
D C |
15.设不等式2x-1>m(x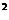 -1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
-1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
14.设函数f(x)=lg(ax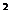 +2x+1).
+2x+1).
(1)若f(x)的定义域是R,求实数a的取值范围;
(2)若f(x)的值域是R,求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com