
29.[安徽省蚌埠市第二次教学质量检查考试(理)22.](本小题满分14分)数列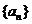 和数列
和数列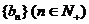 由下列条件确定:
由下列条件确定:
①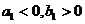 ;
;
②当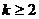 时,
时,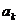 与
与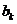 满足如下条件:当
满足如下条件:当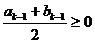 时,
时,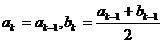 ;当
;当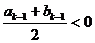 时,
时,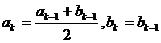 。
。
解答下列问题:
(Ⅰ)证明数列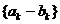 是等比数列;
是等比数列;
(Ⅱ)求数列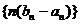 的前n项和为
的前n项和为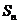 ;
;
(Ⅲ)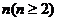 是满足
是满足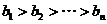 的最大整数时,用
的最大整数时,用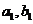 表示n的满足的条件。
表示n的满足的条件。
[解析]:(Ⅰ)当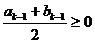 时,
时,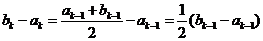
当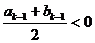 时,
时,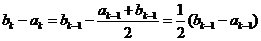
所以不论哪种情况,都有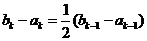 ,又显然
,又显然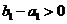 ,
,
故数列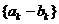 是等比数列
是等比数列
(Ⅱ)由(Ⅰ)知,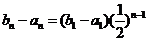 ,故
,故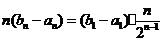
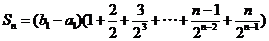
所以,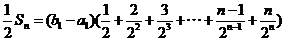
所以,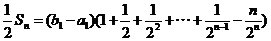 ,
,
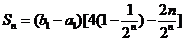
(Ⅲ)当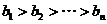
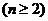 时,
时,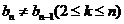
由②知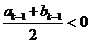 不成立,故
不成立,故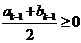 从而对于
从而对于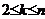 ,有
,有 ,于是
,于是 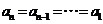 ,故
,故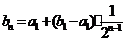
若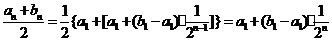 ,
,
若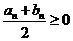 ,则
,则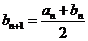
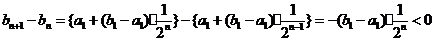
所以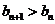 ,这与n是满足
,这与n是满足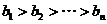
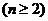 的最大整数矛盾。
的最大整数矛盾。
因此n是满足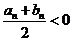 的最小整数,
的最小整数,
而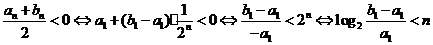
因而,n是满足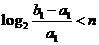 最小整数
最小整数
28.[天津市汉沽一中2008~2009届第六次月考 (理)22.](本小题满分14分)已知函数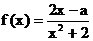 (x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程
(x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程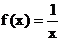 的两实数根为x1、x2.
的两实数根为x1、x2.
试问:
是否存在实数m,使得不等式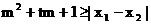 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
[解析]:
(Ⅰ) 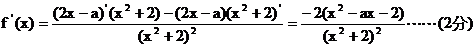
因为函数f(x)在区间[-1,1]上是增函数,所以f‘(x)≥0在区间x∈[-1,1]恒成立
即有x2-ax-2≤0在区间[-1,1]上恒成立。 构造函数g(x)=x2-ax-2
∴满足题意的充要条件是: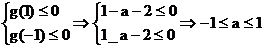
所以所求的集合A[-1,1] ………(7分)
(Ⅱ)由题意得: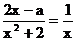 得到:x2-ax-2=0………(8分)
得到:x2-ax-2=0………(8分)
因为△=a2+8>0 所以方程恒有两个不等的根为x1、x2由根与系数的关系有: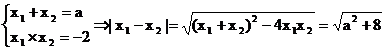 ……(9分)
……(9分)
因为a∈A即a∈[-1,1],所以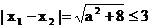 要使不等式
要使不等式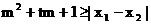 对任意a∈A及t∈[-1,1]恒成立,当且仅当
对任意a∈A及t∈[-1,1]恒成立,当且仅当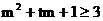 对任意的t∈[-1,1]恒成立……(11分)
对任意的t∈[-1,1]恒成立……(11分)
构造函数φ(x)=m2+tm-2=mt+(m2-2) ≥0对任意的t∈[-1,1]恒成立的充要条件是
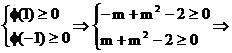 m≥2或m≤-2.故存在实数m满足题意且为
m≥2或m≤-2.故存在实数m满足题意且为
{m| m≥2或m≤-2}为所求 (14分)
27.[2009年深圳市高三年级第一次调研考试(理)21.](本题满分14分)已知函数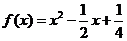 ,
,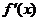 为函数
为函数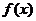 的导函数.
的导函数.
(Ⅰ)若数列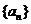 满足:
满足: ,
,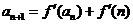 (
(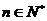 ),求数列
),求数列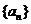 的通项
的通项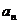 ;
;
(Ⅱ)若数列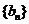 满足:
满足: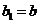 ,
,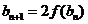 (
(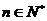 ).
).
ⅰ.当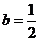 时,数列
时,数列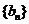 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列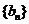 的通项
的通项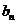 ;若不是,请说明理由;
;若不是,请说明理由;
ⅱ.当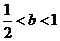 时, 求证:
时, 求证: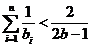 .
.
[解析]:(Ⅰ)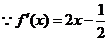 ,
…………………1分
,
…………………1分
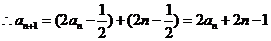 ,
,
即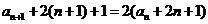 .
…………………………3分
.
…………………………3分
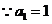 ,
, 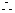 数列
数列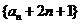 是首项为
是首项为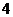 ,公比为
,公比为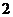 的等比数列.
的等比数列.
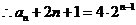 ,即
,即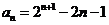 .
…………………………5分
.
…………………………5分
(Ⅱ)(ⅰ)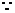
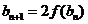
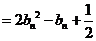 ,
,
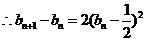 .
.
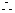 当
当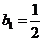 时,
时,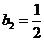 .
.
假设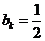 ,则
,则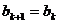 .
.
由数学归纳法,得出数列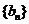 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为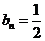 . …………8分
. …………8分
(ⅱ)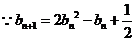 ,
,
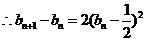 .
.
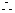 当
当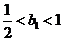 时,
时,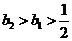 .
.
假设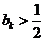 ,则
,则
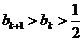 .
.
由数学归纳法,得出数列
 .
…………………………10分
.
…………………………10分
又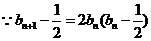 ,
,
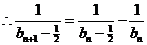 ,
,
即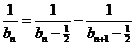 .
…………………………12分
.
…………………………12分
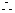
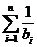
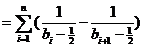
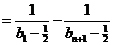 .
.
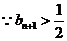 ,
,
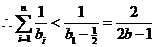 .
…………………………14分
.
…………………………14分
26.[江门市2009年高考模拟考试(理)21.](本小题满分12分)已知函数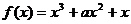 ,
,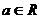 是常数,
是常数,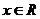 .
.
⑴若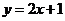 是曲线
是曲线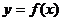 的一条切线,求
的一条切线,求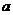 的值;
的值;
⑵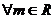 ,试证明
,试证明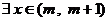 ,使
,使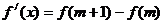 .
.
[解析]:⑴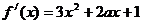 -------1分,解
-------1分,解 得,
得,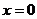 或
或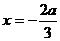 -------2分
-------2分
当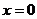 时,
时,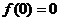 ,
,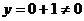 ,所以
,所以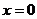 不成立-------3分
不成立-------3分
当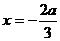 时,由
时,由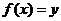 ,即
,即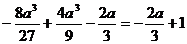 ,得
,得 -----5分
-----5分
⑵作函数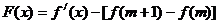 -------6分
-------6分
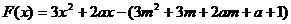 ,函数
,函数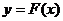 在
在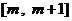 上的图象是一条连续不断的曲线------7分,
上的图象是一条连续不断的曲线------7分,
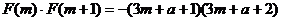 ------8分
------8分
①若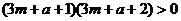 ,
,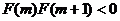 ,
,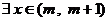 ,使
,使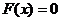 ,
,
即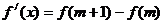 -------10分
-------10分
②若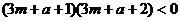 ,
,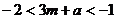 ,
,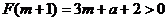 ,
,
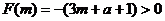 ,
,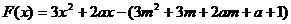 当
当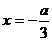 时有最小值
时有最小值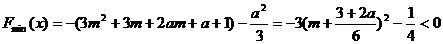 ,且当
,且当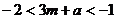 时
时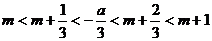 -------11分,
-------11分,
所以存在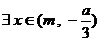 (或
(或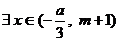 )从而
)从而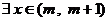 ,使
,使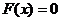 ,即
,即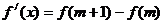 -------12分
-------12分
25.[江门市2009年高考模拟考试(文)21.](本小题满分14分)设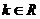 ,函数
,函数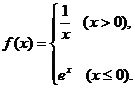 ,
,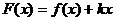 ,
,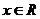 .
.
⑴当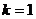 时,求
时,求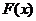 的值域;
的值域;
⑵试讨论函数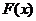 的单调性.
的单调性.
[解析]:⑴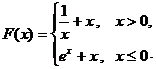 ----------1分,
----------1分,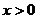 时,
时,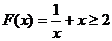 ----------2分;
----------2分;
当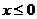 时,
时,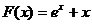 ,根据指数函数与幂函数的单调性,是单调递增函数--------3分,
,根据指数函数与幂函数的单调性,是单调递增函数--------3分,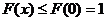 -------4分。所以
-------4分。所以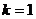 时,
时,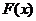 的值域为
的值域为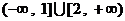 -------5分。
-------5分。
⑵依题意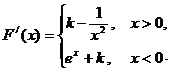 --
---6分。
--
---6分。
①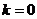 ,当
,当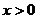 时,
时,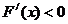 ,
,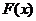 递减,当
递减,当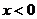 时,
时,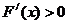 ,
,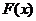 递增 ----8分。
递增 ----8分。
②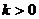 ,当
,当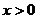 时,解
时,解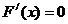 得
得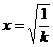 ,当
,当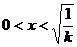 时,
时,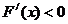 ,
,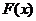 递减,当
递减,当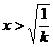 时,
时,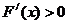 ,
,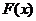 递增。当
递增。当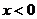 时,
时,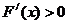 ,
,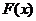 递增--
---10分。
递增--
---10分。
③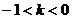 ,当
,当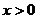 时,
时,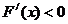 ,
,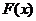 递减。当
递减。当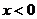 时,解
时,解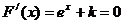 得
得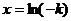 ,当
,当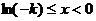 时,
时,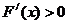 ,
,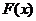 递增,当
递增,当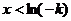 时,
时,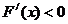 ,
,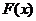 递减-----12分。
递减-----12分。
④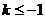 ,对任意
,对任意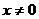 ,
,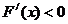 ,
,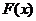 在每个定义域区间上递减---
--13分。
在每个定义域区间上递减---
--13分。
综上所述,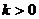 时,
时,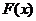 在
在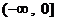 或
或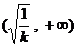 上单调递增,在
上单调递增,在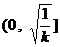 上单调递减;
上单调递减;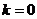 时,
时,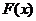 在
在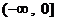 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;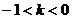 时,
时,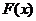 在
在 上单调递增,在
上单调递增,在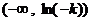 或
或 上单调递减;
上单调递减;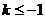 时,
时,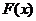 在每个定义域区间上递减---- -14分。
在每个定义域区间上递减---- -14分。
24.[广东省茂名市2009年第一次高考模拟考试(理)21.](本小题满分14分)
已知数列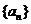 ,
, ,
,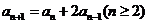
(Ⅰ)求数列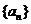 的通项公式
的通项公式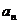
(Ⅱ)当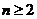 时,求证:
时,求证: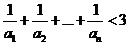
(Ⅲ)若函数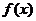 满足:
满足: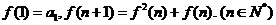
求证: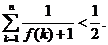
[解析]: (1) 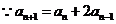 ,两边加
,两边加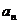 得:
得: 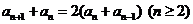 ,
,
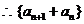 是以2为公比,
是以2为公比, 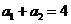 为首项的等比数列.
为首项的等比数列. 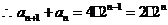 ……①
……①
由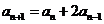 两边减
两边减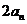 得:
得: 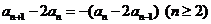
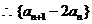 是以
是以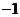
为公比, 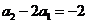 为首项的等比数列.
为首项的等比数列. 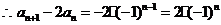 ……②
……②
①-②得: 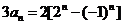 所以,所求通项为
所以,所求通项为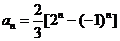 …………5分
…………5分
(2) 当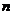 为偶数时,
为偶数时,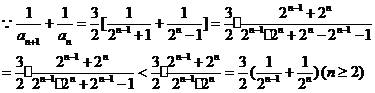
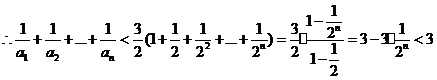
当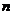 为奇数时,
为奇数时,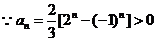 ,
,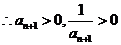 ,又
,又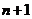 为偶数
为偶数
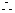 由(1)知,
由(1)知, 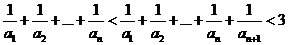 ……………………10分
……………………10分
(3)证明: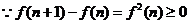
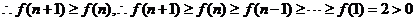
又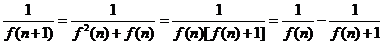
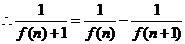 ……12分
……12分
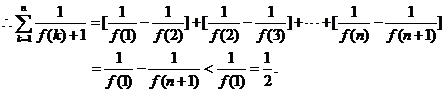 ………………-14分
………………-14分
23.[中山市2009届高三第二学期2月四校联考(理)](本小题满分14分,第Ⅰ小题5分,第Ⅱ小题4分,第Ⅲ小题5分).
数列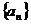 的各项均为正数,
的各项均为正数,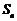 为其前
为其前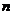 项和,对于任意
项和,对于任意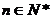 ,总有
,总有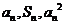 成等差数列.
成等差数列.
(Ⅰ)求数列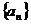 的通项公式;
的通项公式;
(Ⅱ)设数列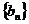 的前
的前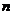 项和为
项和为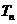 ,且
,且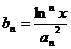 ,求证:对任意实数
,求证:对任意实数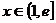 (
(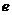 是常数,
是常数,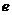 =2.71828
=2.71828 )和任意正整数
)和任意正整数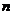 ,总有
,总有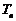
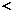 2;
2;
(Ⅲ) 正数数列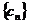 中,
中,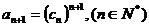 .求数列
.求数列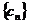 中的最大项.
中的最大项.
[解析]:(Ⅰ)解:由已知:对于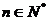 ,总有
,总有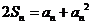 ①成立
①成立
∴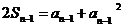 (n ≥ 2)② …………………1分
(n ≥ 2)② …………………1分
①--②得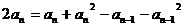
∴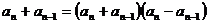
∵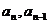 均为正数,∴
均为正数,∴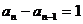 (n ≥ 2)
(n ≥ 2)
∴数列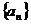 是公差为1的等差数列
………3分
是公差为1的等差数列
………3分
又n=1时,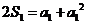 ,
解得
,
解得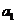 =1
=1
∴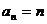 .(
.(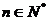 ) ……………………………………………5分
) ……………………………………………5分
(Ⅱ)证明:∵对任意实数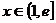 和任意正整数n,总有
和任意正整数n,总有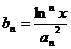 ≤
≤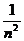 .……6分
.……6分
∴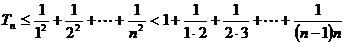
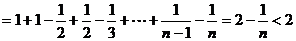 ……………9分
……………9分
(Ⅲ)解:由已知 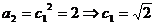 ,
,
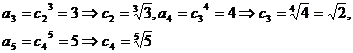
易得 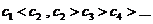
猜想 n≥2 时,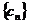 是递减数列. ………………………………11分
是递减数列. ………………………………11分
令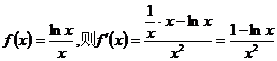
∵当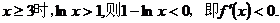
∴在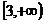 内
内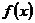 为单调递减函数.
为单调递减函数.
由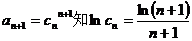 .
.
∴n≥2 时, 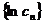 是递减数列.即
是递减数列.即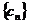 是递减数列.
是递减数列.
又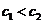 , ∴数列
, ∴数列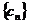 中的最大项为
中的最大项为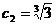 . …………………………14分
. …………………………14分
22.[2009年3月四县(市)高三调研考试.(理)21.]本小题满分13分)
已知函数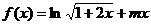
(1)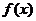 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数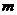 的取值范围
的取值范围
(2)当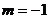 时,求函数
时,求函数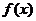 的最大值
的最大值
(3)当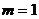 时,且
时,且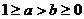 ,证明:
,证明: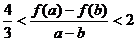
[解析]:(1)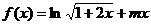 ,
,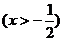 ∴
∴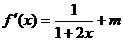
因为对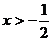 ,有
,有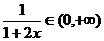
∴不存在实数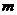 使
使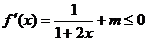 ,对
,对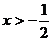 恒成立
2分
恒成立
2分
由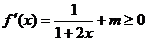 恒成立,∴
恒成立,∴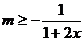 ,
,
而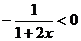 ,所以
,所以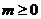
经检验,当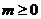 时,
时,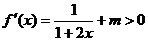 对
对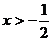 恒成立。
恒成立。
∴当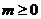 时,
时,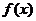 为定义域上的单调增函数
4分
为定义域上的单调增函数
4分
(2)当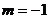 时,由
时,由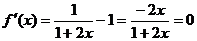 ,得
,得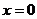
当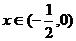 时,
时,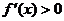 ,当
,当 时,
时,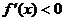
∴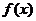 在
在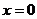 时取得最大值,∴此时函数
时取得最大值,∴此时函数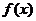 的最大值为
的最大值为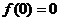 7分
7分
(3)由(2)得,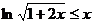 对
对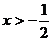 恒成立,当且仅当
恒成立,当且仅当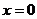 时取等号
时取等号
当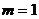 时,
时,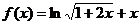 ,∵
,∵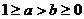 ,
,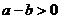
∴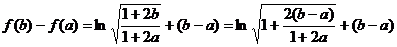
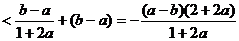
∴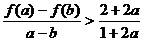
同理可得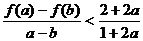 ,
,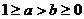 ,
,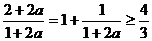 ,
,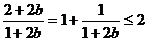
∴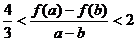
法二:当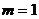 时(由待证命题的结构进行猜想,辅助函数,求差得之),
时(由待证命题的结构进行猜想,辅助函数,求差得之),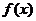 在
在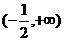 上递增
上递增
令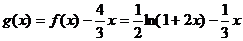
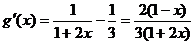 在
在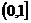 上总有
上总有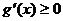 ,即
,即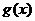 在
在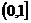 上递增
上递增
当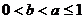 时,
时,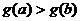
即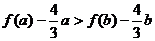
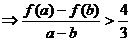
令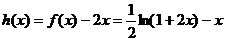 由(2)它在
由(2)它在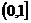 上递减 ∴
上递减 ∴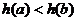
即
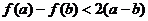 ∵
∵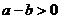
∴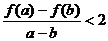 ,综上
,综上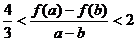 成立,其中
成立,其中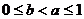 。
。
21.[2009年3月四县(市)高三调研考试.(文)21.](本小题满分13分)设三次函数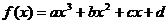
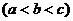 ,在
,在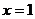 处取得极值,其图像在
处取得极值,其图像在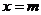 处的切线的斜率为
处的切线的斜率为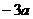 。
。
(1)求证: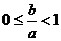 ;
;
(2)若函数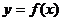 在区间
在区间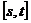 上单调递增,求
上单调递增,求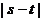 的取值范围。
的取值范围。
[解析]:(1)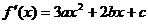 ,由题设,得
,由题设,得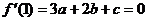 ①
①
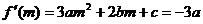 ②
②
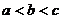 ,
,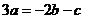 ∴
∴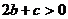
∵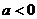 , ∴
, ∴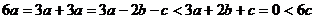 ,∴
,∴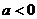 ,
,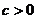
由①代入②得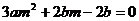 ,∴
,∴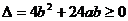 ,
,
得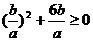 ,∴
,∴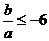 或
或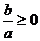 ③
③
将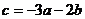 代入
代入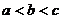 中,得
中,得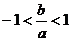 ④
④
由③、④得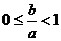 ;
7分
;
7分
(2)由(1)知,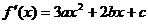
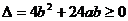 ,
,
∴方程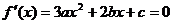 的判别式有两个不等实根
的判别式有两个不等实根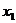 ,
,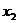 ,
,
又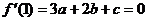 ,∴
,∴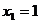 ,
,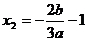 ,
,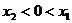 ,
,
当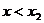 或
或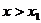 时,
时,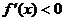 ,当
,当 时,
时,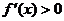
∴函数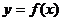 单调增区间是
单调增区间是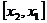 ,∴
,∴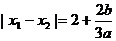 ,
,
由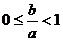 知
知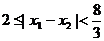 。
。
∵函数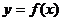 在区间
在区间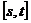 上单调递增,∴
上单调递增,∴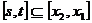 ,
,
∴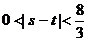 ,即
,即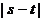 的取值范围是
的取值范围是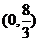 。 13分
。 13分
20.[2009届山东省实验中学高三年级第四次综合测试(理)22.](本小题满分13分) 已知函数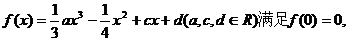
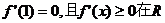 上恒成立.
上恒成立.
(1)求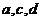 的值;
的值;
(2)若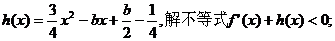
(3)是否存在实数m,使函数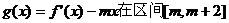 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
[解析]:(1)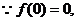
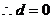
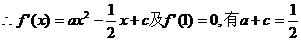
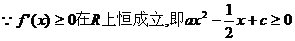 恒成立
恒成立
即 恒成立
恒成立
显然 时,上式不能恒成立
时,上式不能恒成立
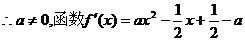 是二次函数
是二次函数
由于对一切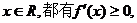 于是由二次函数的性质可得
于是由二次函数的性质可得
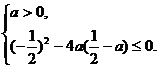
即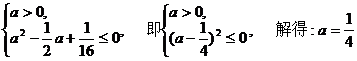
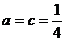 .
.
(2)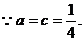
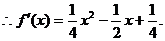
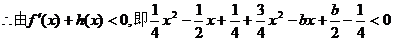
即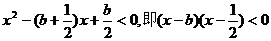
当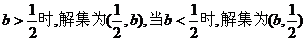 ,当
,当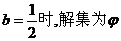 .
.
(3)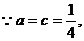
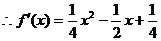

该函数图象开口向上,且对称轴为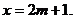
假设存在实数m使函数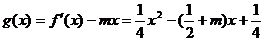 区间
区间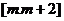 上有
上有
最小值-5.
①当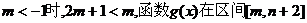 上是递增的.
上是递增的.
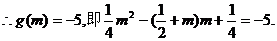
解得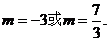
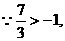
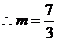 舍去
舍去
②当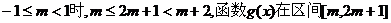 上是递减的,而在
上是递减的,而在
区间 上是递增的,
上是递增的, 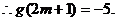
即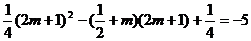
解得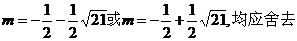
③当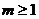 时,
时,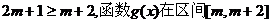 上递减的
上递减的
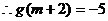 即
即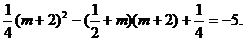
解得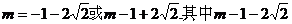 应舍去.
应舍去.
综上可得,当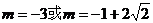 时,
时,
函数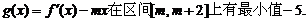
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com