
例1.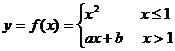 在
在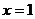 处可导,则
处可导,则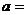
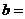
思路: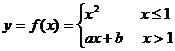 在
在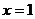 处可导,必连续
处可导,必连续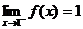
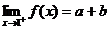
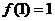 ∴
∴
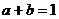
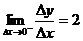
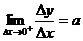 ∴
∴
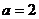
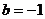
例2.已知f(x)在x=a处可导,且f′(a)=b,求下列极限:
(1)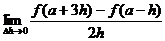 ; (2)
; (2)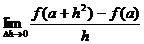
分析:在导数定义中,增量△x的形式是多种多样,但不论△x选择哪种形式,△y也必须选择相对应的形式。利用函数f(x)在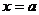 处可导的条件,可以将已给定的极限式恒等变形转化为导数定义的结构形式。
处可导的条件,可以将已给定的极限式恒等变形转化为导数定义的结构形式。
解:(1)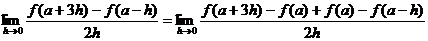
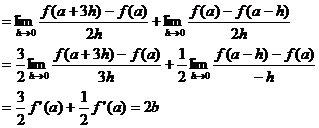
(2)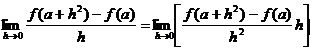
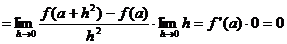
说明:只有深刻理解概念的本质,才能灵活应用概念解题。解决这类问题的关键是等价变形,使极限式转化为导数定义的结构形式。
例3.观察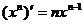 ,
,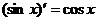 ,
,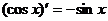 ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
解:若 为偶函数
为偶函数 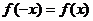 令
令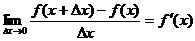
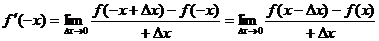
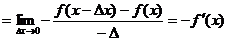
∴ 可导的偶函数的导函数是奇函数
另证: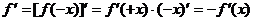
∴ 可导的偶函数的导函数是奇函数
例4.(1)求曲线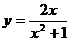 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;
(2)运动曲线方程为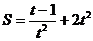 ,求t=3时的速度。
,求t=3时的速度。
分析:根据导数的几何意义及导数的物理意义可知,函数y=f(x)在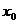 处的导数就是曲线y=f(x)在点
处的导数就是曲线y=f(x)在点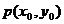 处的切线的斜率。瞬时速度是位移函数S(t)对时间的导数。
处的切线的斜率。瞬时速度是位移函数S(t)对时间的导数。
解:(1)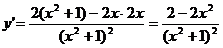 ,
,
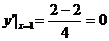 ,即曲线在点(1,1)处的切线斜率k=0
,即曲线在点(1,1)处的切线斜率k=0
因此曲线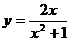 在(1,1)处的切线方程为y=1
在(1,1)处的切线方程为y=1
(2)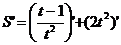
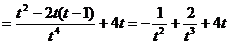
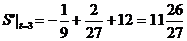 。
。
例5. 求下列函数单调区间
(1)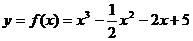
(2)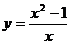
(3)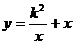
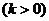
(4)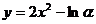
解:(1)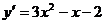
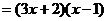
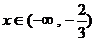
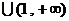 时
时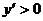
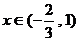
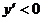 ∴
∴ 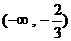 ,
,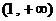
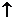
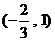
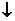
(2)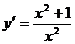 ∴
∴ 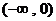 ,
,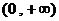
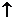
(3)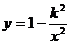
∴ 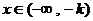
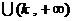
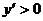
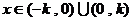
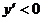
∴ 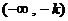 ,
,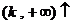
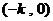 ,
,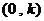
(4)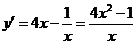 定义域为
定义域为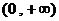
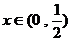
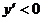
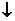
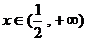
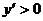
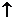
例6.求证下列不等式
(1)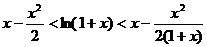
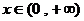
(2)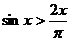
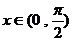
(3)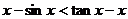
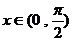
证:(1)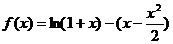
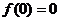
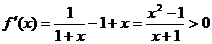
∴ 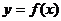 为
为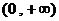 上
上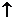 ∴
∴ 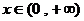
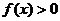 恒成立
恒成立
∴ 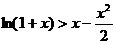
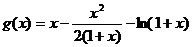
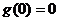
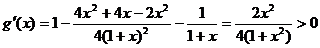
∴
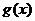 在
在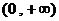 上
上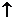 ∴
∴ 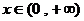
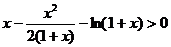 恒成立
恒成立
(2)原式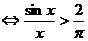 令
令 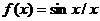
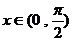
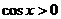
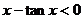
∴ 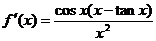 ∴
∴ 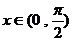
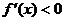
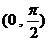
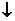
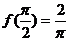 ∴
∴ 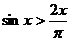
(3)令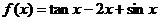
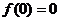
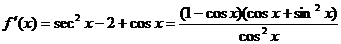
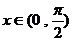
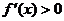 ∴
∴ 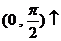
∴
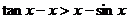
例7.利用导数求和:
(1)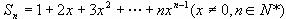 ;
;
(2)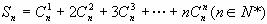 。
。
分析:这两个问题可分别通过错位相减法及利用二项式定理来解决。转换思维角度,由求导公式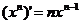 ,可联想到它们是另外一个和式的导数,利用导数运算可使问题的解决更加简捷。
,可联想到它们是另外一个和式的导数,利用导数运算可使问题的解决更加简捷。
解:(1)当x=1时,
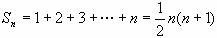 ;
;
当x≠1时,
∵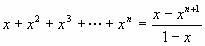 ,
,
两边都是关于x的函数,求导得
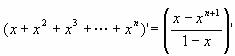
即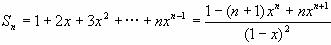
(2)∵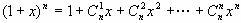 ,
,
两边都是关于x的函数,求导得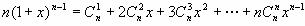 。
。
令x=1得
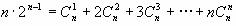 ,
,
即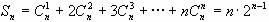 。
。
例8.求满足条件的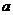
(1)使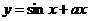 为
为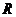 上增函数
上增函数
(2)使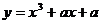 为
为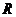 上……
上……
(3)使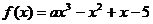 为
为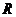 上
上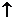
解:(1)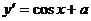 ∴
∴ 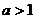
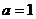 时
时 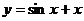 也成立 ∴
也成立 ∴ 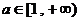
(2)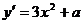
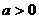
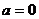 时
时 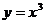 也成立 ∴
也成立 ∴ 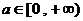
(3)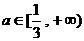
例9.(1)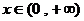 求证
求证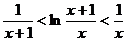
(2)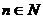
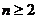 求证
求证 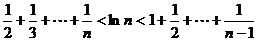
(1)证:令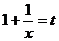
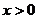 ∴
∴ 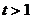
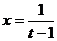
原不等式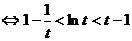 令
令 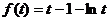 ∴
∴ 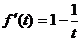
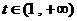
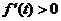 ∴
∴ 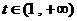
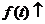 ∴
∴ 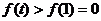
∴ 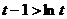 令
令 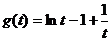 ∴
∴ 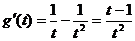
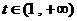
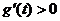 ∴
∴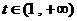
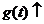
∴ 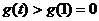 ∴
∴ 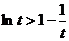 ∴
∴ 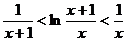
(2)令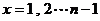 上式也成立
上式也成立
将各式相加 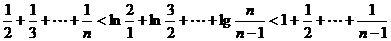
即 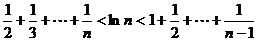
例10.(2003年普通高等学校招生全国统一考试(天津卷,理工农医类19))
设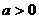 ,求函数
,求函数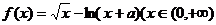 的单调区间.
的单调区间.
分析:本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力.
解: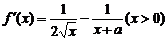 .
.
当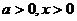 时
时 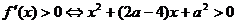 .
.
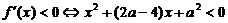
(i)当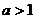 时,对所有
时,对所有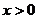 ,有
,有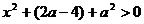 .
.
即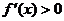 ,此时
,此时 在
在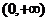 内单调递增.
内单调递增.
(ii)当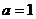 时,对
时,对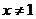 ,有
,有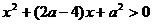 ,
,
即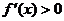 ,此时
,此时 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数 在x=1处连续,因此,
在x=1处连续,因此,
函数 在(0,+
在(0,+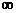 )内单调递增
)内单调递增
(iii)当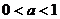 时,令
时,令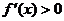 ,即
,即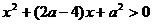 .
.
解得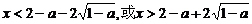 .
.
因此,函数 在区间
在区间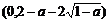 内单调递增,在区间
内单调递增,在区间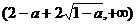
内也单调递增.
令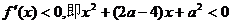 ,
,
解得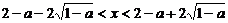 .
.
因此,函数 在区间
在区间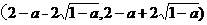 内单调递减.
内单调递减.
说明:本题用传统作差比较法无法划分函数的单调区间,只有用导数才行,这是教材新增的内容。其理论依据如下(人教版试验本第三册P148):
设函数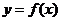 在某个区间内可导,如果
在某个区间内可导,如果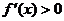 ,则
,则 为增函数;如果
为增函数;如果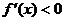 ,则
,则 为减函数。如果
为减函数。如果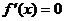 ,则
,则 为常数。
为常数。
例11.已知抛物线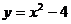 与直线y=x+2相交于A、B两点,过A、B两点的切线分别为
与直线y=x+2相交于A、B两点,过A、B两点的切线分别为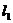 和
和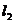 。
。
(1)求A、B两点的坐标;
(2)求直线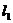 与
与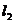 的夹角。
的夹角。
分析:理解导数的几何意义是解决本例的关键。
解 (1)由方程组
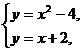
解得 A(-2,0),B(3,5)
(2)由y′=2x,则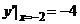 ,
,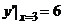 。设两直线的夹角为θ,根据两直线的夹角公式,
。设两直线的夹角为θ,根据两直线的夹角公式,
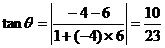
所以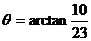
说明:本例中直线与抛物线的交点处的切线,就是该点处抛物线的切线。注意两条直线的夹角公式有绝对值符号。
例12.(2001年天津卷)设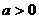 ,
,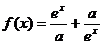 是
是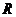 上的偶函数。
上的偶函数。
(I)求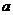 的值;
的值;
(II)证明 在
在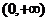 上是增函数。
上是增函数。
解:(I)依题意,对一切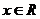 有
有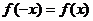 ,即
,即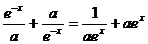 ,
,
∴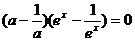 对一切
对一切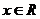 成立,
成立,
由此得到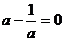 ,
,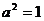 ,
,
又∵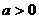 ,∴
,∴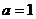 。
。
(II)证明:由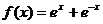 ,得
,得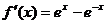
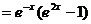 ,
,
当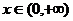 时,有
时,有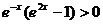 ,此时
,此时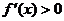 。
。
∴ 在
在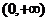 上是增函数。
上是增函数。
例13.(2000年全国、天津卷)设函数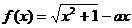 ,其中
,其中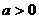 。
。
(I)解不等式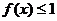 ;
;
(II)证明:当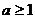 时,函数
时,函数 在区间
在区间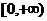 上是单调函数。
上是单调函数。
解1:(I)分类讨论解无理不等式(略)。
(II)作差比较(略)。
解2: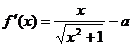
(i)当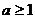 时,有
时,有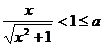 ,此时
,此时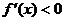 ,函数
,函数 在区间
在区间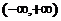 上是单调递减函数。但
上是单调递减函数。但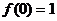 ,因此,当且仅当
,因此,当且仅当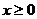 时,
时,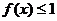 。
。
(ii)当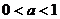 时,解不等式
时,解不等式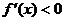 ,得
,得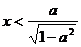 ,
, 在区间
在区间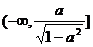 上是单调递减函数。
上是单调递减函数。
解方程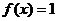 ,得
,得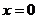 或
或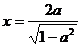 ,
,
∵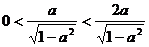 ,
,
∴当且仅当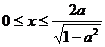 时,
时,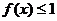 ,
,
综上,(I)当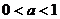 时,所给不等式的解集为:
时,所给不等式的解集为: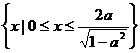 ;
;
当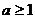 时,所给不等式的解集为:
时,所给不等式的解集为: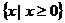 。
。
(II)当且仅当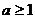 时,函数
时,函数 在区间
在区间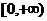 上时单调函数。
上时单调函数。
例14.(2002年普通高等学校招生全国统一考试(新课程卷理科类20))
已知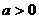 ,函数
,函数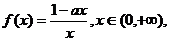 设
设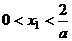 ,记曲线
,记曲线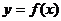 在点
在点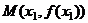 处的切线为
处的切线为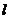 。
。
(Ⅰ)求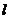 的方程;
的方程;
(Ⅱ)设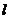 与
与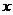 轴的交点为
轴的交点为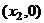 ,证明:①
,证明:①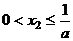 ②若
②若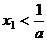 ,则
,则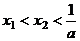
解:(1) 的导数
的导数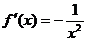 ,由此得切线
,由此得切线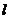 的方程
的方程
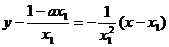 ,
,
(2)依题得,切线方程中令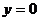 ,得
,得
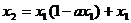
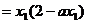 ,其中
,其中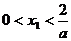 ,
,
(ⅰ)由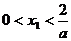 ,
,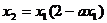 ,有
,有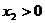 ,及
,及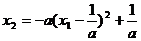 ,
,
∴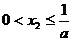 ,当且仅当
,当且仅当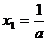 时,
时,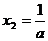 。
。
(ⅱ)当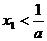 时,
时,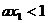 ,因此,
,因此,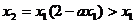 ,且由(ⅰ),
,且由(ⅰ),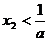 ,
,
所以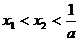 。
。
例15.(2003年普通高等学校招生全国统一考试(江苏卷21))
已知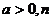 为正整数.
为正整数.
(Ⅰ)设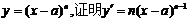 ;
;
(Ⅱ)设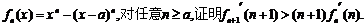
分析:本小题主要考查导数、不等式证明等知识,考查综合运用所数学知识解决问题的能力。
证明:(Ⅰ)因为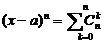
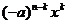 ,
,
所以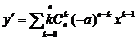
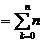
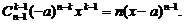
(Ⅱ)对函数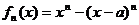 求导数:
求导数:
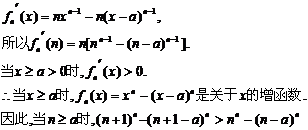
∴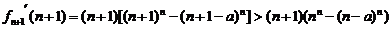
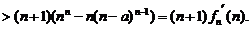
即对任意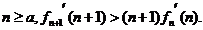
4.求复合函数的导数,一般按以下三个步骤进行:
(1)适当选定中间变量,正确分解复合关系;
(2)分步求导(弄清每一步求导是哪个变量对哪个变量求导);
(3)把中间变量代回原自变量(一般是x)的函数。
也就是说,首先,选定中间变量,分解复合关系,说明函数关系y=f(μ),μ=f(x);然后将已知函数对中间变量求导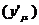 ,中间变量对自变量求导
,中间变量对自变量求导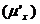 ;最后求
;最后求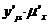 ,并将中间变量代回为自变量的函数。整个过程可简记为分解--求导--回代。熟练以后,可以省略中间过程。若遇多重复合,可以相应地多次用中间变量。
,并将中间变量代回为自变量的函数。整个过程可简记为分解--求导--回代。熟练以后,可以省略中间过程。若遇多重复合,可以相应地多次用中间变量。
3.要能正确求导,必须做到以下两点:
(1)熟练掌握各基本初等函数的求导公式以及和、差、积、商的求导法则,复合函数的求导法则。
(2)对于一个复合函数,一定要理清中间的复合关系,弄清各分解函数中应对哪个变量求导。
2.利用导数判别可导函数的极值的方法及求一些实际问题的最大值与最小值.
复合函数的求导法则是微积分中的重点与难点内容。课本中先通过实例,引出复合函数的求导法则,接下来对法则进行了证明。
对于复合函数,以前我们只是见过,没有专门定义和介绍过它,课本中以描述性的方式对复合函数加以直观定义,使我们对复合函数的的概念有一个初步的认识,再结合以后的例题、习题就可以逐步了解复合函数的概念。
1.导数概念的理解.
12. 
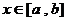
(1)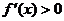 恒成立 ∴
恒成立 ∴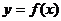 为
为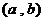 上
上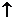
∴ 对任意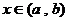 不等式
不等式 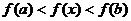 恒成立
恒成立
(2)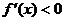 恒成立 ∴
恒成立 ∴ 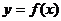 在
在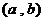 上
上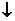
∴ 对任意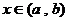 不等式
不等式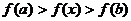 恒成立
恒成立
11. 导数与函数的单调性的关系
㈠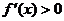 与
与 为增函数的关系。
为增函数的关系。
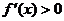 能推出
能推出 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数 在
在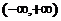 上单调递增,但
上单调递增,但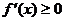 ,∴
,∴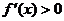 是
是 为增函数的充分不必要条件。
为增函数的充分不必要条件。
㈡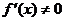 时,
时,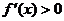 与
与 为增函数的关系。
为增函数的关系。
若将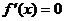 的根作为分界点,因为规定
的根作为分界点,因为规定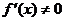 ,即抠去了分界点,此时
,即抠去了分界点,此时 为增函数,就一定有
为增函数,就一定有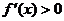 。∴当
。∴当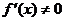 时,
时,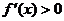 是
是 为增函数的充分必要条件。
为增函数的充分必要条件。
㈢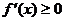 与
与 为增函数的关系。
为增函数的关系。
 为增函数,一定可以推出
为增函数,一定可以推出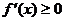 ,但反之不一定,因为
,但反之不一定,因为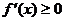 ,即为
,即为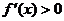 或
或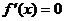 。当函数在某个区间内恒有
。当函数在某个区间内恒有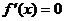 ,则
,则 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴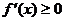 是
是 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,要谨慎处理。
㈣单调区间的求解过程,已知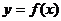
(1)分析
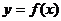 的定义域; (2)求导数
的定义域; (2)求导数 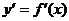
(3)解不等式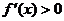 ,解集在定义域内的部分为增区间
,解集在定义域内的部分为增区间
(4)解不等式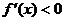 ,解集在定义域内的部分为减区间
,解集在定义域内的部分为减区间
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数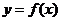 在某个区间内可导。
在某个区间内可导。
㈤函数单调区间的合并
函数单调区间的合并主要依据是函数 在
在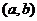 单调递增,在
单调递增,在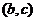 单调递增,又知函数在
单调递增,又知函数在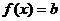 处连续,因此
处连续,因此 在
在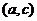 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
10.商的导数
两个函数的商的求导法则,课本中未加证明,只要求记住并能运用就可以。现补充证明如下:
设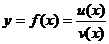
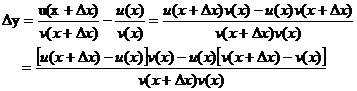
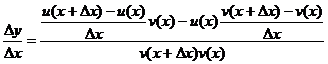
因为v(x)在点x处可导,所以它在点x处连续,于是△x→0时,v(x+△x)→v(x),从而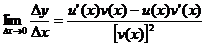 即
即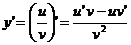 。
。
说明:(1)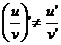 ; (2)
; (2)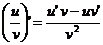
学习了函数的和、差、积、商的求导法则后,由常函数、幂函数及正、余弦函数经加、减、乘、除运算得到的简单的函数,均可利用求导法则与导数公式求导,而不需要回到导数的定义去求。
8.和(或差)的导数
上一节我们学习了常见函数的导数公式,那么对于函数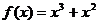 的导数,又如何求呢?我们不妨先利用导数的定义来求。
的导数,又如何求呢?我们不妨先利用导数的定义来求。
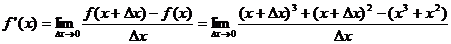
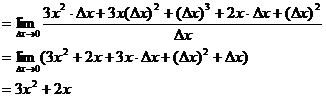
我们不难发现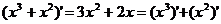 ,即两函数和的导数等于这两函数的导数的和。
,即两函数和的导数等于这两函数的导数的和。
由此我们猜测在一般情况下结论成立。事实上教材中证明了我们的猜想,这就是两个函数的和(或差)的求导法则。
9.积的导数
两个函数的积的求导法则的证明是本节的一个难点,证明过程中变形的关键是依据导数定义的结构形式。(具体过程见课本P120)
说明:
(1)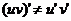 ;
;
(2)若c为常数,则(cu) ′=cu′。
7.导数的几何意义
函数y=f(x)在点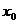 处的导数,就是曲线y=(x)在点
处的导数,就是曲线y=(x)在点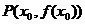 处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步:
处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步:
(1)求出函数y=f(x)在点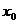 处的导数,即曲线y=f(x)在点
处的导数,即曲线y=f(x)在点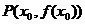 处的切线的斜率;
处的切线的斜率;
(2)在已知切点坐标和切线斜率的条件下,求得切线方程为
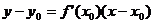
特别地,如果曲线y=f(x)在点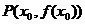 处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为
处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为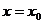
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com