
6.设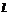 ,
,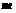 ,
,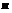 表示三条直线,
表示三条直线,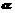 ,
,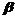 ,
,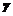 表示三个平面,给出下列四个命题:
表示三个平面,给出下列四个命题:
①若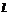 ⊥
⊥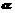 ,
,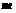 ⊥
⊥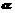 ,则
,则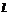 ∥
∥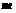 ;
;
②若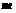
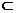
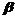 ,
,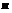 是
是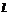 在
在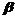 内的射影,
内的射影,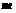 ⊥
⊥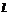 ,则
,则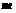 ⊥
⊥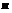 ;
;
③若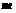
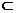
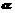 ,
,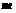 ∥
∥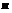 ,则
,则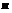 ∥
∥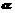 ;
;
④若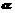 ⊥
⊥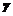 ,
,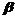 ⊥
⊥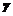 ,则
,则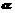 ∥
∥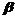 . 其中真命题为( )
. 其中真命题为( )
A.①② B.①②③ C.①②③④ D.③④
4.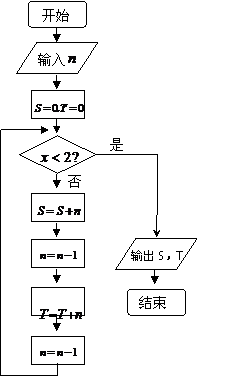 在等比数列
在等比数列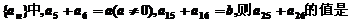 ( )
( )
A.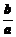 B.
B.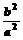 C、
C、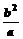 D.
D.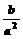
3.棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为( )
A.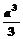 B.
B. 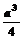 C.
C.
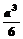 D.
D. 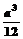
2.设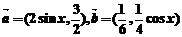 ,且
,且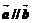 ,则锐角
,则锐角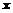 为( )
为( )
A.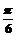 B.
B.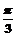 C.
C.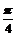 D.
D.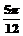
1、复数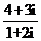 的实部是( )
的实部是( )
A.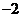 B.
B.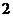 C.3 D.
C.3 D.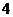
34.(2002年普通高等学校招生全国统一考试(新课程卷文史类21))
已知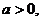 函数
函数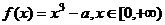 ,设
,设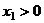 ,记曲线
,记曲线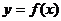 在点
在点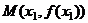 处的切线为
处的切线为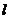 。
。
(Ⅰ)求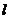 的方程;
的方程;
(Ⅱ)设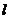 与
与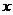 轴的交点为
轴的交点为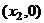 ,证明:①
,证明:①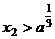 ;②若
;②若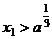 ,则
,则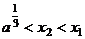 。
。
33.证明:如果函数y=f(x)在点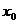 处可导,那么函数y=f(x)在点
处可导,那么函数y=f(x)在点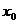 处连续。
处连续。
32.(1)求函数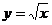 在x=1处的导数;
在x=1处的导数;
(2)求函数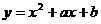 (a、b为常数)的导数。
(a、b为常数)的导数。
31.
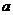 、
、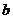 、
、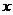 、
、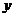 均为正数 且
均为正数 且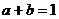
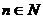
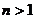
求证: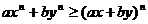
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com