
21.(本小题满分14分)
(Ⅰ)已知函数: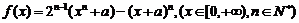 求函数
求函数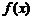 的最小值;
的最小值;
(Ⅱ)证明: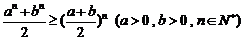 ;
;
(Ⅲ)定理:若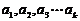 均为正数,则有
均为正数,则有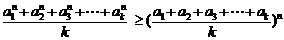 成立(其中
成立(其中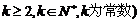 .请你构造一个函数
.请你构造一个函数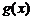 ,证明:
,证明:
当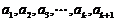 均为正数时,
均为正数时,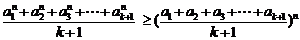 .
.
20.( 本小题满分14分)
已知动圆Q经过点A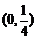 ,且与直线
,且与直线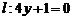 相切,动圆圆心Q的轨迹为曲线C,过定点
相切,动圆圆心Q的轨迹为曲线C,过定点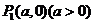 作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点
作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点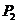 ,再过
,再过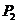 作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点
作与y轴平行的直线且和C相交于点M2,又过点M2作C的切线和x轴交于点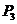 ,如此继续下去直至无穷,记△
,如此继续下去直至无穷,记△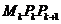 的面积为
的面积为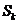
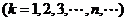

(Ⅰ)求曲线C的方程;
(Ⅱ)试求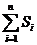 的值。
的值。
19. (本小题满分14分)
设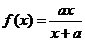
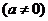 ,令
,令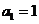 ,
,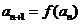 ,又
,又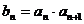 ,
,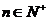 .
.
(Ⅰ)判断数列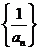 是等差数列还是等比数列并证明;
是等差数列还是等比数列并证明;
(Ⅱ)求数列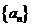 的通项公式;
的通项公式;
(Ⅲ)求数列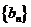 的前
的前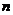 项和.
项和.
18.(本小题满分14分)
甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
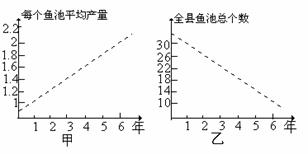
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只。
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个。
请你根据提供的信息说明:
(Ⅰ)第2年全县鱼池的个数及全县出产的鳗鱼总数。
(Ⅱ)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?说明理由。
(Ⅲ)哪一年的规模(即总产量)最大?说明理由。
17.(本小题满分12分)
如图(1),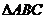 是等腰直角三角形,
是等腰直角三角形,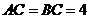 ,
,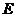 、
、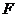 分别为
分别为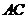 、
、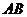 的中点,将
的中点,将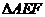 沿
沿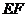 折起,使
折起,使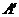 在平面
在平面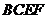 上的射影
上的射影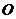 恰为
恰为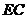 的中点,得到图(2).
的中点,得到图(2).
 (Ⅰ)求证:
(Ⅰ)求证: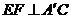 ;
;
 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥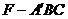 的体积.
的体积.
图(1) 图(2)
16.(本小题满分12分)
已知复数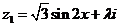 ,
,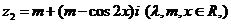 ,且
,且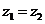 .
.
(Ⅰ)若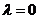 且
且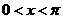
 ,求
,求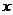 的值;
的值;
(Ⅱ)设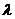 =
=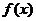 ,求
,求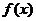 的最小正周期和单调增区间.
的最小正周期和单调增区间.
15.(几何证明选讲选做题) 15、如图,PA切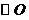 于点A,割线PBC经过圆心O,OB=PB=1, OA绕点O逆时针旋转60°到OD,则PD的长为
.
于点A,割线PBC经过圆心O,OB=PB=1, OA绕点O逆时针旋转60°到OD,则PD的长为
.
14、 (坐标系与参数方程选做题) 曲线的极坐标方程
(坐标系与参数方程选做题) 曲线的极坐标方程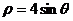 化为直角坐标方程为
.
化为直角坐标方程为
.
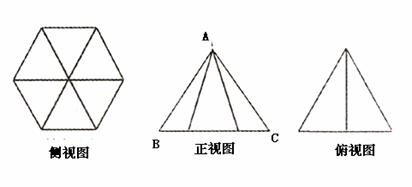
13、下表给出一个“直角三角形数阵”:满足每一列成等
差数列,从第三行起,每一行的数成等比数列,且每一行
的公比相等,记第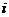 行第
行第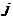 列的数为
列的数为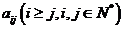 ,
,
11、将5个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有 .
 12、一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为
.
12、一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com