
5.用数学归纳法证明:an+1+(a+1)2n -1可以被a2+a+1整除(n∈N).
4.用数学归纳法证明(n+1)(n+2)…(n+n)=2n´1´2´3´…(2n─1)(n∈N),从“k到k+1”左端应增乘的代数式为 .
3.当n为正奇数时,求证xn+yn被x+y整除,当第二步假设n=2k─1时命题为真,进而需验证n= ,命题为真。
2.平面上有n条直线,且任何两条不平行,任何三条不过同一点,该n条直线把平面分成f(n) 个区域,则f(n+1)=f(n)+ .
1.由归纳原理分别探求:
(1)凸n边形的内角和f(n)= ;
(2)凸n边形的对角线条数f(n)= ;
(3)平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)= .
23.设a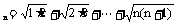 (n=1,2,3……),b
(n=1,2,3……),b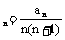 (n=1,2,3……),
(n=1,2,3……),
用极限定义证明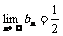 .(85年)
.(85年)
练习(数学归纳法)
22.已知直线L:x─ny=0(n∈N),圆M:(x+1)2+(y+1)2=1,抛物线φ:y=(x─1)2,又L与M
交于点A、B,L与φ交于点C、D,求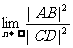 .
.
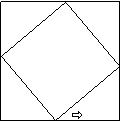
21.在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接
正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
20.已知数列a1,a2,……an,……的前项和Sn与an的关系是Sn=-ban+1-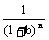 ,其中b是与n无关的常数,且b≠-1;
,其中b是与n无关的常数,且b≠-1;
Ⅰ.求an和an+1的关系式;
Ⅱ.写出用n和b表示an的表达式;
Ⅲ.当0<b<1时,求极限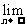 Sn.(87年)
Sn.(87年)
19.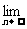
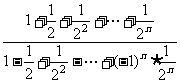 .=
.
.=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com